Dinâmica de Rotação
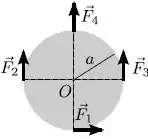
Um disco fino e homogêneo de raio encontra-se em repouso sobre uma superfície horizontal sem atrito. Num dado instante aplicam-se na periferia do disco três forças tangenciais e uma radial, todas de mesma intensidade com direções, sentidos e pontos de aplicação conforme indicados na figura. Nesse instante, o módulo do torque resultante em relação ao centro do disco é
- ;
- ;
- ;
- ;
- ;
Passo 1
O torque da força vai ser zero porque o vetor força e o vetor são paralelos, ambos estão na direção vertical, dessa forma, o ângulo entre eles é nulo, e já que o torque é dado por:
E , temos que somente as outras forças terão toques não nulos.
Todas as outras forças tem braço igual ao raio do disco, isso porque são todas perpendiculares ao disco. Então
Resposta
Letra C
Exercícios de Livros Relacionados
Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2