Sistema de Partículas
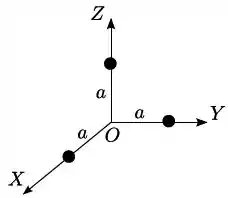
Um sistema é constituído de três partículas de mesma massa localizadas nos semi-eixos positivos , e a uma mesma distância da origem, como indica a figura. O vetor posição do centro de massa do sistema é
- ;
- ;
- ;
- ;
- ;
Passo 1
O eixo cartesiano já foi dado pelo enunciado, então vamos nos basear nele.
Repara que o arranjo é composto por 3 partículas, vamos numera-los para nos organizar.
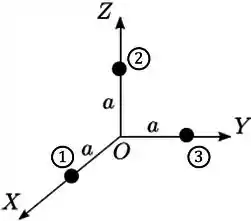
Passo 2
Vamos ter
Nessa questão temos o centro de massa em dimensões, não tem problema, basta resolver como está indicado na teoria, a logica não muda só vai aparecer mais uma componente.
Passo 3
Usando a fórmula para as coordenadas do centro de massa vamos ter
Lembrando que ele possuem a mesma massa, mas não foi dado no enunciado, vamos fazer
Então
Passo 4
Agora fazendo no
Então
Passo 5
Agora fazendo no
Então
Passo 6
Escrevendo esse centro de massa vetorialmente teremos
Colocando em evidência teremos
Resposta
Letra B