P3 de Física 1 da UNICAMP - 2017.2 Diurno

Uma extremidade de um fio de de comprimento é fixa, e a outra é ligada a uma pedra de . A pedra descreve uma circunferência vertical, passando pelo ponto mais alto com uma velocidade de . A tração no fio (em newtons) nesse ponto é aproximadamente:

Dado:

A.

B.

C.

D.

E.

Um carro viaja com velocidade constante em uma pista circular horizontal. No diagrama abaixo, é a força de resistência do ar sobre o carro. Qual das outras forças mostradas melhor representa a força horizontal da pista sobre os pneus do carro?

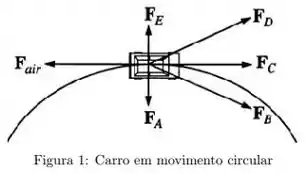
A.

B.

C.

D.

E.

Num movimento circular uniforme de raio igual a metros, uma partícula descreve um deslocamento angular de radianos em segundos. Qual a distância percorrida (em metros) pela partícula e a frequência do movimento em (Hertz)?

A. e

B. e

C. e

D. e

E. e

Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:

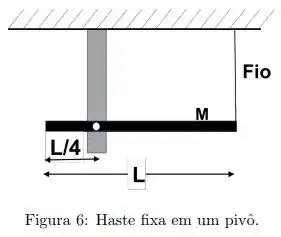
(a) Dado que o momento de inércia em relação ao eixo de rotação perpendicular a haste e passando pelo centro de massa é , determine o momento de inércia da haste relativo ao pivô de rotação em .

Entradas e rampas de saída circulares em rodovias são frequentemente elevadas, para permitir que um veículo circule nelas com velocidade de até . Para projetar uma rampa semelhante que suporte uma velocidade de , deve-se:

A. aumentar o raio por um fator de ;

B. diminuir o raio por um fator de ;

C. diminuir o raio por um fator de ;

D. aumentar o raio por um fator de ;

E. aumentar o raio por um fator de ;

Um disco de momento de inércia gira em torno de um eixo vertical com velocidade angular . Um segundo disco, com momento de inércia e inicialmente sem girar, cai sobre o primeiro, conforme a figura 2. Por causa do atrito entre os discos, eles finalmente atingem a mesma velocidade angular . A razão vale:

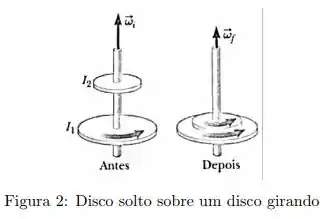
A.

B.

C.

D.

E.

Uma haste rígida de massa e comprimento pode girar sem atrito em torno do seu centro fixo , como na figura. Duas partículas de massas e são presas às suas extremidades. Este sistema gira em torno do ponto , num plano vertical, com uma velocidade angular instantânea . O módulo do momento angular do sistema é:

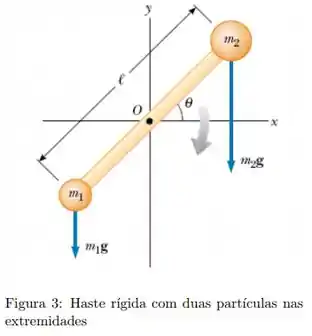
Dados: Momento de inércia de uma barra uniforme (massa , comprimento ) em relação ao eixo que passa pelo centro de massa e é perpendicular ao comprimento da barra: .

A.

B.

C.

D.

E.

Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:

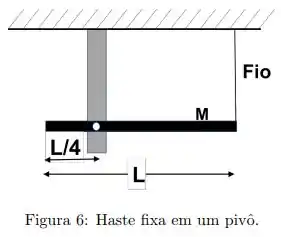
Em um dado momento o fio é cortado e a haste fica livre para girar em torno do eixo.

Dados: Momento de inércia em relação ao eixo de rotação perpendicular a haste e passando pelo pivô é

(d) Determine o momento angular da haste relativo ao pivô no momento em que a haste alcança a posição vertical.

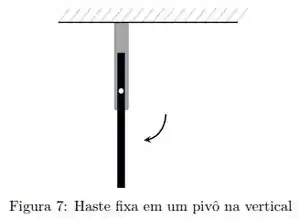
Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:

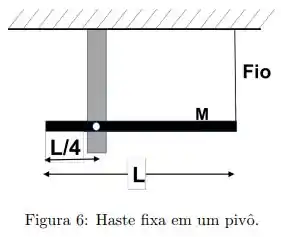
Em um dado momento o fio é cortado e a haste fica livre para girar em torno do eixo.

Dados: Momento de inércia em relaç��o ao eixo de rotação perpendicular a haste e passando pelo pivô é

(c) Calcule a aceleração angular da haste no momento que o fio é cortado.

Sobre um rolamento sem deslizamento de um cilindro sobre o chão, é correto dizer que:

A. a velocidade do centro de massa é independente da velocidade angular;

B. a velocidade escalar do ponto mais alto do cilindro é menor que a velocidade do centro de massa;

C. a velocidade escalar do ponto mais alto do cilindro é maior que a velocidade do centro de massa;

D. a velocidade escalar do ponto mais alto do cilindro é igual à velocidade do centro de massa;

E. a velocidade do ponto de contato com o chão é vezes a velocidade do centro de massa.

Considere um automóvel com tração dianteira. Quando o carro acelera, em que sentido aponta a força de atrito, , na roda dianteira e, , na roda traseira, respectivamente?

Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:

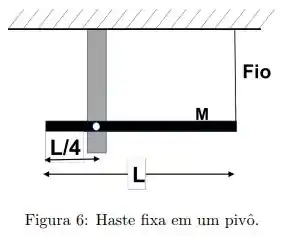
(b) Calcule a tensão, no fio que suporta a haste.

Duas massas, uma com massa e outra com massa , estão presas a uma haste rígida horizontal muito leve, como mostrado na Figura 4. Quando o sistema é liberado a partir do repouso, a haste começa a girar em torno de um eixo perpendicular à página com uma aceleração angular de:

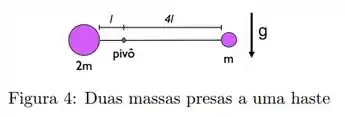
A.

B.

C.

D.

E.

Um aro de massa e raio está em repouso no topo de um plano inclinado, como mostrado. O aro rola plano abaixo sem deslizar. Quando ele atinge a base do plano seu momento angular em torno de seu centro de massa é:

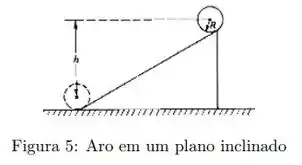
Dados: Momento de inércia de um anel uniforme (massa , raio ) em relação ao eixo que passa pelo centro de massa e é perpendicular ao plano do anel: .

A.

B.

C.

D.

E.

Marque a alternativa incorreta:

A. O trabalho da força centrípeta é sempre zero.

B. A força de atrito nunca pode ser uma força centrípeta.

C. Quando o movimento circular não é uniforme, a aceleração só tem componente centrípeta.

D. A velocidade num movimento circular, uniforme ou não, é um vetor ortogonal ao vetor distância ao centro da trajetória.

E. A aceleração angular instantâne é sempre igual à derivada da velocidade angular pelo tempo.

Considere a seguinte expressão para o vetor aceleração linear de uma partícula de um corpo rígido em rotação em torno de um eixo fixo: , onde é vetor posição da partícula com relação ao eixo de rotação, é o vetor velocidade linear da partícula, é o vetor velocidade angular de rotação, e é o vetor aceleração angular. Tendo em mente o movimento e a trajetória da partícula, marque a alternativa incorreta ( significa módulo de ):

A. Na expressão da aceleração, o termo é ortogonal ao termo .

B. O termo do vetor aceleração é responsável por fazer variar .

C. O termo do vetor aceleração é responsável por fazer variar .

D. O termo do vetor aceleração é responsável por alterar a direção do vetor .

E. O termo do vetor aceleração é responsável por alterar a direção do vetor .