Uma haste rígida de massa e comprimento pode girar sem atrito em torno do seu centro fixo , como na figura. Duas partículas de massas e são presas às suas extremidades. Este sistema gira em torno do ponto , num plano vertical, com uma velocidade angular instantânea . O módulo do momento angular do sistema é:

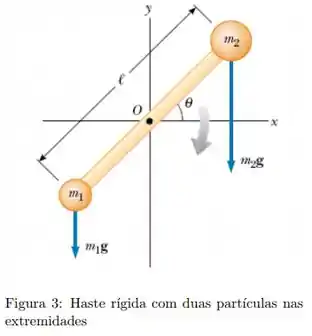
Dados: Momento de inércia de uma barra uniforme (massa , comprimento ) em relação ao eixo que passa pelo centro de massa e é perpendicular ao comprimento da barra: .

A.

B.

C.

D.

E.

O momento de inércia do sistema será a soma dos momentos de inércia de cada elemento do sistema.

Temos uma partícula de massa , uma partícula de massa e uma haste de massa , então:

O momento de inércia de uma partícula é dado pela sua massa vezes a distância ao eixo de rotação ao quadrado:

Tanto para a partícula de massa quanto para a partícula de massa , temos uma distância ao eixo de rotação igual à metade do comprimento da haste:

Enquanto isso, o momento de inércia da haste com relação a um eixo perpendicular passando pelo seu centro de massa (centro da haste) é tabelado:

Onde o comprimento da haste é :

Substituindo esses valores, conseguimos o momento de inércia do sistema:

Agora, basta voltarmos a expressão do momento angular:

Pronto, agora para ajeitar a resposta podemos fazer colocar tudo sobre o mesmo denominador:

Ficamos com a letra B.