Sobre um rolamento sem deslizamento de um cilindro sobre o chão, é correto dizer que:
A. a velocidade do centro de massa é independente da velocidade angular;
B. a velocidade escalar do ponto mais alto do cilindro é menor que a velocidade do centro de massa;
C. a velocidade escalar do ponto mais alto do cilindro é maior que a velocidade do centro de massa;
D. a velocidade escalar do ponto mais alto do cilindro é igual à velocidade do centro de massa;
E. a velocidade do ponto de contato com o chão é vezes a velocidade do centro de massa.
Passo 1
Primeiro de tudo, um rolamento é a soma de um movimento de translação com um movimento de rotação.
Movimento de translação:
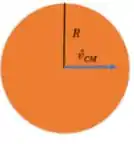
No movimento de translação, todos os pontos apresentam uma velocidade igual à velocidade do centro de massa:
Movimento de rotação:
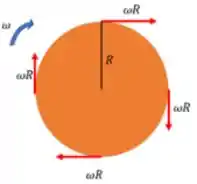
Enquanto no movimento de rotação, todos os pontos apresentam uma velocidade dada pela velocidade angular do corpo vezes sua distância ao eixo de rotação :
Juntando esses dois movimentos temos o rolamento.
Assim, a velocidade total de cada ponto será a soma das velocidades de translação com a de rotação:
Passo 2
Com essa relação podemos encontrar algumas características específicas de um rolamento sem deslizamento.
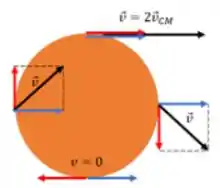
Para o ponto de contato com o chão,se não há deslizamento sua velocidade total é zero.
Então, sua velocidade de translação (azul) se anula com sua velocidade de rotação (vermelho):
Opaa, então vimos que a velocidade do centro de massa está amarrada à velocidade angular para que o ponto de contato não deslize.
Assim, já podemos eliminar as alternativas A. e E.
Passo 3
E para o ponto superior?
Podemos calcular a velocidade total desse ponto com a mesma relação:
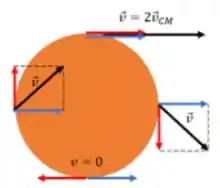
Para o ponto na parte de cima, as velocidades de translação e de rotação apontam no mesmo sentido, então:
Mas como achamos a relação:
Podemos dizer que a velocidade do ponto superior é:
Então a velocidade escalar no ponto superior ao cilindro realmente é maior que a velocidade do centro de massa quando não há deslizamento.
Assim, achamos a letra C. como resposta.
Resposta
Letra C.