Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
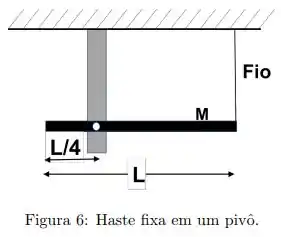
Em um dado momento o fio é cortado e a haste fica livre para girar em torno do eixo.
Dados: Momento de inércia em relação ao eixo de rotação perpendicular a haste e passando pelo pivô é
(d) Determine o momento angular da haste relativo ao pivô no momento em que a haste alcança a posição vertical.
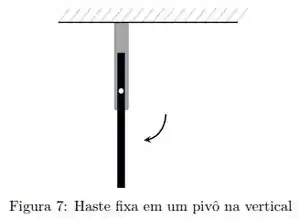
Passo 1
O momento angular é dado por:
Já temos o momento de inércia, porém, não temos a velocidade angular .
Como podemos achar isso?
Vamos lá...
No momento em que o fio é cortado, temos apenas as duas forças atuando sobre a haste... peso e normal :
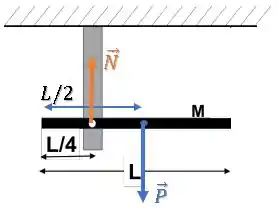
Como a força normal está aplicada em um ponto que não tem translação, seu trabalho é nulo:
Assim, ela não retira energia do sistema mesmo sendo uma força não-conservativa.
Já a força peso realiza um certo trabalho, porém ela é uma força conservativa. Então ela realiza trabalho convertendo energia potencial em cinética. Ou seja, também não vai retirar energia do sistema.
Logo podemos dizer que a energia mecânica do sistema se conserva:
Com isso conseguimos achar a velocidade angular , quando a barra estiver vertical e calcular finalmente o momento angular que queremos.
Passo 2
Vamos à conservação.
Inicialmente temos apenas energia potencial gravitacional:
E na parte de baixo, vamos considerar uma energia potencial gravitacional nula, então temos apenas energia cinética de rotação:
Então, nossa equação fica assim:
Mas quem é essa altura ?
Passo 3
Essa altura será a altura que o centro de massa desceu:
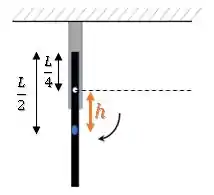
Passo 4
Então, temos que:
Substituindo o valor do momento de inércia, temos:
Cortando :
Passo 5
Agora que temos , podemos calcular :
Substituindo os valores, temos:
Podemos entrar com os números na raiz para simplificar:
Resposta
(d)