Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
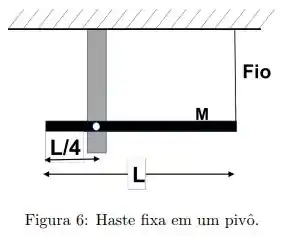
(b) Calcule a tensão, no fio que suporta a haste.
Passo 1
Primeiro de tudo, vamos localizar a posição do centro de massa dessa barra.
Como a haste é longa e fina, vamos considerar que a massa é uniformemente distribuida.
Assim, temos que o centro de massa se localiza no centro da haste. Ou seja, à uma distância da extremidade da barra:
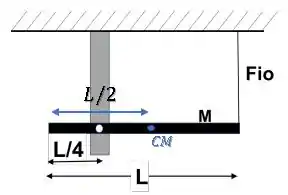
Logo, a distância entre os eixos que passam pelo centro de massa e pelo pivô será:
Passo 2
Okay, pra que fizemos isso?
Ah, porque agora podemos analisar as forças sobre a haste, incluindo a força peso:
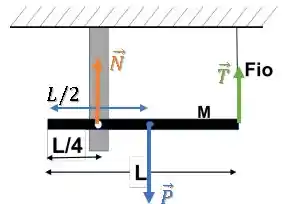
Como a haste está em equilíbrio, temos duas condições:
Mas repara que escrevendo a equação de equilíbrio de forças, teremos duas incógnitas:
Como não conhecemos nem a força Normal , nem a força de tração , não conseguimos resolver o problema.
Assim, vamos recorrer ao torque...
Vamos calcular o torque resultante com relação ao pivô, pois dessa maneira o torque de é nulo e não entra na equação:
Como já dito, a força normal está aplicada no próprio eixo de rotação, assim seu torque é nulo:
Passo 3
Vamos calcular esses torques.
Além disso, vamos definir o sentido anti-horário como positivo e horário como negativo, por uma questão de escolha mesmo.
Como a força peso está perpendicular ao braço de alavanca (distância ao eixo), seu torque será dado pela distância ao eixo vezes a força peso. Já o seu sentido, será negativo, já que a força tenta girar a haste no sentido horário:
Enquanto isso, o torque da força de tração também será dado pelo módulo da distância ao eixo vezes o módulo da força, já que ela também é perpendicular ao braço de alavanca:
O sentido agora será positivo, já que a força tenta girar a haste no sentido anti-horário.
Já a distância do ponto de aplicação à força será dado pelo comprimento todo da barra menos o comprimento da extremidade após o pivô :
Assim, o torque da força de tração será:
Passo 4
Voltando ao somatório de torques, temos:
Assim, encontramos o valor da força de tração no fio.
Resposta
(b)