Um aro de massa e raio está em repouso no topo de um plano inclinado, como mostrado. O aro rola plano abaixo sem deslizar. Quando ele atinge a base do plano seu momento angular em torno de seu centro de massa é:
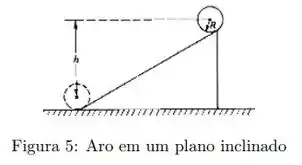
Dados: Momento de inércia de um anel uniforme (massa , raio ) em relação ao eixo que passa pelo centro de massa e é perpendicular ao plano do anel: .
A.
B.
C.
D.
E.
Passo 1
Queremos o momento angular do aro no instante em que ele chega ao plano.
Podemos calcular o momento angular com a seguinte expressão:
Já temos o momento de inércia de um aro com relação a um eixo passando pelo seu centro:
Porém, ainda não sabemos a velocidade angular .
Para isso, podemos tentar ir pelo caminho de energia...
Mas será que a energia mecânica se conserva?
Passo 2
Existem forças atuando sobre o aro, a pergunta é se alguma delas retira energia do sistema.
Força Peso:
A força peso é uma força conservativa, então ela não retira energia do sistema, apenas converte energia potencial em cinética e vice-versa.
Força Normal:
A força normal é uma força não-conservativa, entretanto, ela está sempre perpendicular à superfície da rampa.
Como o aro se move ao longo da rampa, a força normal será perpendicular ao deslocamento a todo instante e não realizará trabalho.
Então, essa força não retira energia do sistema.
Força de Atrito:
A força de atrito é uma força não-conservativa, porém assim como a força normal, ela também não realiza trabalho.
Isso porque o aro rola sem deslizar, então o ponto de contato onde a força de atrito está aplicado não se move e por isso o trabalho é nulo.
Assim, essa força também não retira energia do sistema.
Ouuuuuu sejaaaaa...
A energia mecânica do sistema se conserva!!!

Passo 3
Vamos achar a velocidade angular a partir da conservação da energia mecânica e depois encontrar o momento angular .
A energia mecânica inicial está toda na forma de potencial gravitacional , pois o aro tem velocidade zero:
Enquanto a energia final estará na forma tanto de energia cinética de rotação quanto energia cinética de translação :
Essas energias cinéticas podem ser calculadas com:
Então, temos:
Assim, a conservação ficará:
Substituindo o momento de inércia do aro:
Cortando as massas:
Porém, também não temos o valor de velocidade do centro de massa , né?
Passo 4
Não conhecemos seu valor, mas conseguimos relacioná-lo com , já que é um rolamento sem deslizamento a partir de :
Substituindo isso dentro da expressão, temos:
Passo 5
Por fim, conseguimos o valor do momento angular com o momento de inércia e a velocidade angular :
Ficamos com a letra A.
Resposta
Letra A.