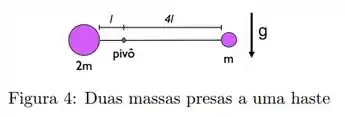
Duas massas, uma com massa e outra com massa , estão presas a uma haste rígida horizontal muito leve, como mostrado na Figura 4. Quando o sistema é liberado a partir do repouso, a haste começa a girar em torno de um eixo perpendicular à página com uma aceleração angular de:

A.

B.

C.

D.

E.

Vamos aos torques do sistema.

As duas partículas terão uma força peso apontando para baixo:

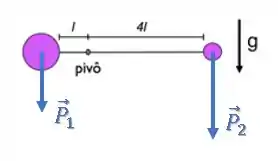
O torque resultante será a soma dos torques de cada uma das forças:

O torque de um força é dado pelo produto vetorial entre o vetor distância ao centro de rotação com o vetor força :

O torque da força peso da partícula 1 é:

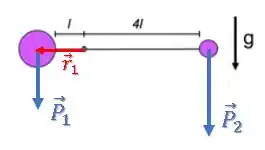
O módulo desse produto vetorial será:

Onde é o ângulo entre os os vetores e .

Como os vetores são perpendiculares, temos um ângulo de entre eles:

Logo, o valor desse torque será o produto dos módulos e , sendo esse torque tentando girar o sistema no sentido horário.

O torque da força peso da partícula 2 é:

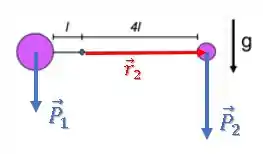
O módulo desse produto vetorial será:

Novamente, como os vetores são perpendiculares, temos um ângulo de entre eles, logo:

Porém, esse torque torque tenta girar o sistema no sentido anti-horário.

Logo ele terá um sentido oposto ao do torque .

O torque resultante será:

Substituindo os valores de distâncias e forças peso, temos:

Como só estamos preocupados com o valor em módulo, podemos tirar esse sinal de menos aí:

Agora vamos encontrar o momento de inércia desse sistema.

Como a haste tem massa desprezível, ela não apresenta momento de inércia, assim, o momento de inércia do sistema será a soma dos momentod de inércia das duas partículas:

O momento de inércia de uma partícula é calculado com:

Sendo a distância da partícula ao eixo.

Assim, temos que:

Agora que já temos tanto o torque resultante como o momento de inércia do sistema , podemos voltar à nossa expressão inicial:

Ficamos com a letra A.