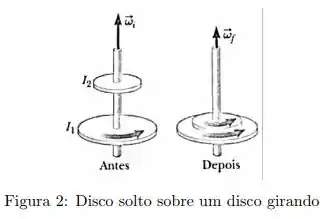
Um disco de momento de inércia gira em torno de um eixo vertical com velocidade angular . Um segundo disco, com momento de inércia e inicialmente sem girar, cai sobre o primeiro, conforme a figura 2. Por causa do atrito entre os discos, eles finalmente atingem a mesma velocidade angular . A razão vale:
A.
B.
C.
D.
E.
Passo 1
Quando o disco parado cai sobre o disco com uma velocidade angular , vai surgir uma força de atrito do disco sobre o disco , tentando fazer o segundo entrar em rotação.
Entretanto, devido à ação e reação, surge também uma força de atrito do disco sobre o disco de mesmo módulo mas sentido oposto, tentando fazer o primeiro diminuir sua velocidade de rotação.
Considerando o nosso sistema como os dois discos juntos, essas forças de atrito são forças internas, uma anula a outra. Assim, seus torques também serão torques internos e também se anulam.
Com isso, como o sistema está livre de torques externos, temos que o momento angular se conserva:
Assim, podemos relacionar as velocidades angulares com os momentos de inércia do sistema para encontrar .
Passo 2
Quem é o momento angular inicial ?
Inicialmente, apenas o disco está em rotação, então o momento angular do sistema será o momento angular do disco 1:
Já no instante após os discos estarem com a mesma velocidade angular , o momento angular do sistema será:
Como o momento de inércia é um quarto de , temos:
Passo 3
Voltando à conservação de momento angular do sistema:
Ficamos com a letra E.
Resposta
Letra E.