Um carro viaja com velocidade constante em uma pista circular horizontal. No diagrama abaixo, é a força de resistência do ar sobre o carro. Qual das outras forças mostradas melhor representa a força horizontal da pista sobre os pneus do carro?
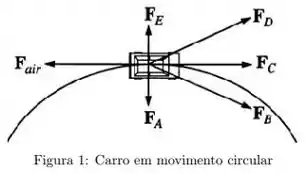
A.
B.
C.
D.
E.
Passo 1
O problema diz o carro percorre uma trajetória circular com velocidade constante, ou seja, ele realiza um movimento circular uniforme.
Vamos dividir as forças na direção radial e tangencial...
Passo 2
Direção radial:
Para um corpo realizar uma trajetória circular, ele deve ter uma componente de sua aceleração apontando para o centro da trajetória sempre com um valor correspondente à força centrípeta.
Então há uma força apontando radialmente para o centro.
Mas essa é a única força atuando além da ?
Passo 3
Direção tangencial:
Para o carro seguir com módulo da velocidade constante, ele não deve ter nenhuma aceleração tangencial, e para isso, a força tangencial resultante deve ser nula...
Porém, já existe uma força de resistência do ar agindo tangencialmente contra o movimento, o que causaria uma componente de aceleração tangencial “para trás”.
Dessa forma, para que o carro possa manter sua velocidade constante, deve existir alguma força também tangencial apontando “para frente” afim de anular a ação da .
Portanto, há uma componente de força tangencial apontando no sentido da velocidade do carro .
Passo 4
Como temos uma componente radial e uma componente tangencial , sua soma vetorial será:
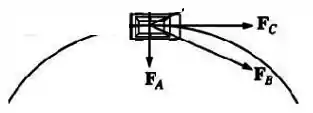
Então a força resultante além de , que é a força agindo sobre os pneus do carro tem a direção de .
Ficamos com a letra B.
Resposta
Letra B.