Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
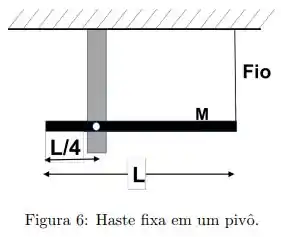
Em um dado momento o fio é cortado e a haste fica livre para girar em torno do eixo.
Dados: Momento de inércia em relaç��o ao eixo de rotação perpendicular a haste e passando pelo pivô é
(c) Calcule a aceleração angular da haste no momento que o fio é cortado.
Passo 1
Queremos a aceleração angular da barra no instante em que cortam o fio.
Quando o fio é cortado, a força de tração irá parar de sustentar a haste e ela começa a entrar em rotação pela ação da força peso.
Podemos calcular a aceleração angular da barra com:
Como já temos o momento de inércia com relação ao eixo de rotação da haste (pivô), basta achar o torque resultante sobre a barra que vamos encontrar .
Passo 2
Vamos analisar as forças sobre a haste.
Há uma força peso aplicada no centro de massa e uma força normal de contato no eixo de rotação.
Qual a posição do centro de massa da haste?
Como a haste é longa e fina, vamos considerar que a massa é uniformemente distribuida.
Assim, temos que o centro de massa se localiza no centro da haste. Ou seja, à uma distância da extremidade da barra:
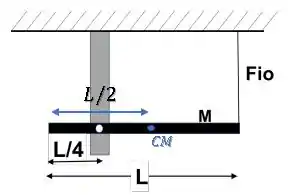
Agora podemos olhar para as forças e sobre a haste:
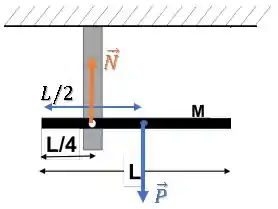
Agora, podemos dizer que o torque resultante será a soma dos torques da força peso e da força normal :
Passo 3
O torque da força peso é dado pelo produto vetorial:
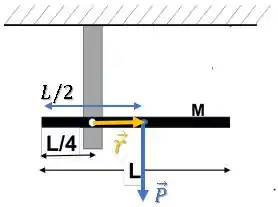
O módulo desse produto vetorial é dado por:
O ângulo entre eles é pois os vetores são perpendiculares, então temos:
A distância é:
Então:
Vamos à força normal ...
Seu torque será:
Como a força está aplicada no próprio eixo de rotação, temos que a distância é nula, então:
Passo 4
Voltando à nossa equação, temos:
Substituindo o valor do momento de inércia, temos:
Cortando a massa e dos dois lados:
Assim, temos:
Resposta
(c)