Considere a seguinte expressão para o vetor aceleração linear de uma partícula de um corpo rígido em rotação em torno de um eixo fixo: , onde é vetor posição da partícula com relação ao eixo de rotação, é o vetor velocidade linear da partícula, é o vetor velocidade angular de rotação, e é o vetor aceleração angular. Tendo em mente o movimento e a trajetória da partícula, marque a alternativa incorreta ( significa módulo de ):
A. Na expressão da aceleração, o termo é ortogonal ao termo .
B. O termo do vetor aceleração é responsável por fazer variar .
C. O termo do vetor aceleração é responsável por fazer variar .
D. O termo do vetor aceleração é responsável por alterar a direção do vetor .
E. O termo do vetor aceleração é responsável por alterar a direção do vetor .
Passo 1
Bom, temos uma partícula em um movimento circular, onde os vetores e são esses aqui:
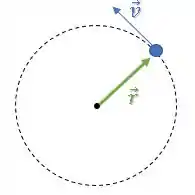
Já os vetores e , ambos são perpendiculares ao plano do movimento. Vamos assumir uma rotação no sentido anti-horário, então pela regra da mão direita, esses dois vetores estão “para cima”:
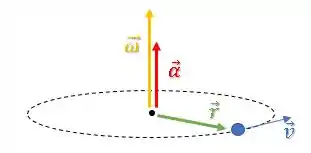
Essa questão trabalha bastante com o conceito de produto vetorial “”...
Um produto vetorial entre dois vetores e , por exemplo, sempre tem como resultado um terceito vetor que é perpendicular aos outros dois.
Agora, vamos definir as direções através desses vetores para facilitar a nossa vida:
Agora, vamos analisar cada alternativa.
Passo 2
A. Na expressão da aceleração, o termo é ortogonal ao termo .
O produto vetorial resulta em um vetor na direção tangencial.
Enquanto o produto vetorial resulta em um vetor na direção radial.
Então, os dois vetores resultantes são realmente ortogonais.
Afirmativa A. está correta.
Passo 3
B. O termo do vetor aceleração é responsável por fazer variar .
Esse produto vetorial resulta em um vetor na direção tangencial, ou seja:
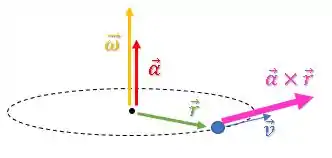
Como essa componente da aceleração (rosa) está na mesma direção da velocidade , seu módulo vai variar.
Afirmativa B. está correta.
Passo 4
C. O termo do vetor aceleração é responsável por fazer variar .
Novamente, temos o vetor rosa como resultado dessa componente:
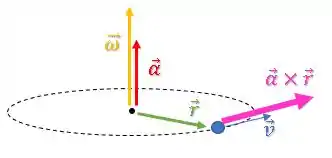
Mas essa aceleração vai fazer o módulo da velocidade angular variar?
Bom, a velocidade angular depende da velocidade linear :
Logo, se como a componente de aceleração tangencial (rosa) faz a velociddade linear variar, a velocidade angular também vai variar.
Afirmativa C. está correta.
Passo 5
D. O termo do vetor aceleração é responsável por alterar a direção do vetor .
A componente da aceleração resultante desse produto vetorial está na direção radial:
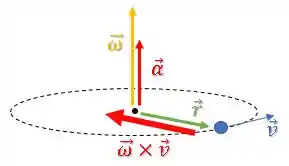
Assim, essa aceleração atua como centrípeta e apenas altera a direção do vetor velocidade , porém sem alterar seu módulo.
Afirmativa D. está correta.
Passo 6
E. O termo do vetor aceleração é responsável por alterar a direção do vetor .
Já vimos que essa componente da aceleração está na direção radial (vermelho):
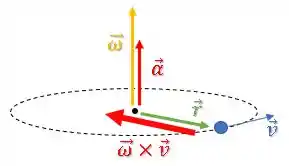
Como essa aceleração funciona como aceleração centrípeta, não alterando o módulo da velocidade , isso significa que a partícula não vai mudar o sentido de rotação devido a essa aceleração.
Como o sentido de está relacionado com a partícula realizar a rotação no sentido horário ou anti-horário, ela não terá sua direção alterada por essa componente da aceleração.
Afirmativa E. está incorreta.
Resposta
Letra (E)