P1 de Física 1 da USP - 2015

A figura mostra uma partícula em movimento circular uniforme que se desloca no sentido anti-horário. As setas enumeradas de 1 a 5 representam a direção de vetores associados a grandezas físicas da dinâmica desta partícula (medidas a partir de um referencial inercial em repouso em relação à trajetória da partícula). Dentre as alternativas a abaixo, assinale aquela que associa corretamente as setas às grandezas físicas descritas, quando a partícula está na posição indicada na figura.

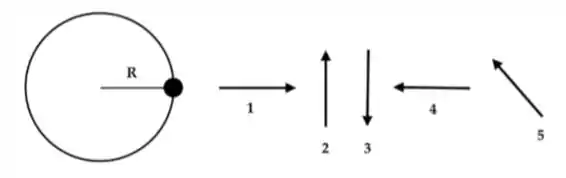
(a) Setas 3 e 4 para a força resultante e velocidade, respectivamente.

(b) Setas 1 e 2 para a força resultante e velocidade, respectivamente.

(c) Setas 1 e 4 para a força resultante e aceleração, respectivamente.

(d) Setas 4 e 2 para a força resultante e velocidade, respectivamente.

(e) Setas 4 e 5 para a força resultante e velocidade, respectivamente.

A figura abaixo mostra um esquema de polias ideais que sustentam os blocos e de massas e , respectivamente. Sabe-se que o bloco de massa movimenta-se para cima com velocidade constante. Sobre as grandezas físicas associadas a este sistema, podemos afirmar:

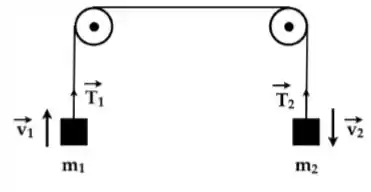
(a)

(b)

(c) e

(d)

(e)

A figura abaixo representa dois blocos e , de massa e , respectivamente, em contato e apoiados sobre uma superfície lisa sem atrito. Uma força é aplicada ao bloco empurrando todo o conjunto. Assinale a alternativa que contém a magnitude (módulo) das forças de contato exercidas pelo bloco 1 sobre o bloco 2 e pelo bloco sobre o bloco .

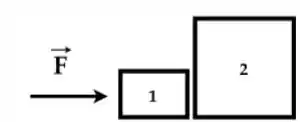
(a) e .

(b) e .

(c) e .

(d) e .

(e) e

Um bloco de massa encontra-se sob um plano inclinado cuja superfície faz um ângulo com a horizontal. Nesta situação, o bloco encontra-se em repouso devido ao atrito estático com a superfície. A inclinação do plano é aumentada por um pequeno ângulo e o bloco começa a deslizar com aceleração de módulo igual a . Sobre os coeficientes de atrito cinético, , e estático, , para a força de atrito entre o bloco e a superfície do plano inclinado podemos afirmar:

(a) e

(b) e

(c) e

(d) e

(e) e

O gráfico abaixo mostra a aceleração de uma partícula como função do tempo:

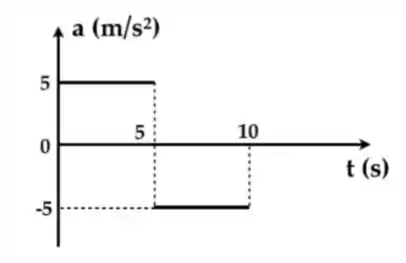
As figuras 1 a 4 abaixo mostram gráficos que podem representar a função posição , ou a velocidade , de uma dada partícula. Dentre as alternativas -, assinale a que corretamente associa os gráficos das figuras 1 a 4 à cinemática da partícula cuja aceleração é dada pelo gráfico acima.

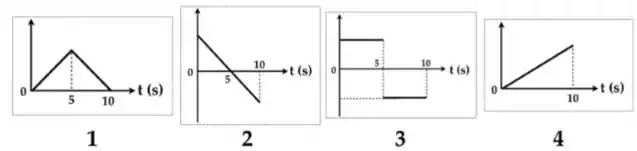
(a) As figuras 1 e 2 representam, respectivamente, a velocidade e posição da partícula como função do tempo.

(b) A figura 4 representa a posição da partícula como função do tempo.

(c) A figura 2 representa a velocidade da partícula como função do tempo.

(d) A figura 1 representa a velocidade da partícula como função do tempo.

(e) As figuras 3 e 4 representam, respectivamente, a velocidade e posição da partícula como função do tempo.

Um bloco de massa desliza sobre um plano inclinado que faz um ângulo com a horizontal. O plano tem uma superfície rugosa, cujo coeficiente de atrito cinético, , é igual a 0,2. O bloco localiza-se inicialmente no topo do plano, a uma altura com a horizontal, e inicia seu movimento a partir do repouso. O plano está montado sobre uma mesa de altura . Ao final do deslizamento ao longo do plano, o bloco cai sob ação da força peso e de uma força de resistência do ar. Veja a figura ao lado para um esquema da situação (use ).

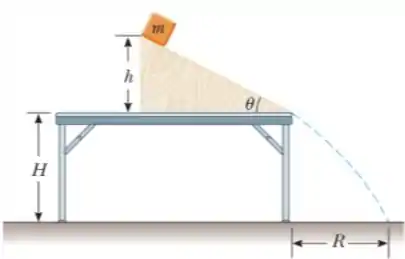
(a) Determine o diagrama de corpo livre (diagrama de forças) para o bloco quando o mesmo inicia seu movimento no topo do plano e outro diagrama para o bloco após o mesmo perder contato com o plano.

(b) Para cada força indicada nestes diagramas, aponte o devido par ação e reação (terceira Lei de Newton) da mesma e discuta seu efeito (escreva no máximo até duas linhas para cada força).

(c) Determine o vetor velocidade do bloco quando o mesmo atinge o final do plano inclinado. Escreva sua resposta na forma .

(d) Ignore a resistência do ar e determine o alcance do bloco. Dica geral: faça substituições numéricas apenas na etapa final das soluções dos itens (c) e (d). Para o item (d), caso você não tenha feito o item (c), deixe a resposta em termos de e .

Duas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrita pelas funções posição , , e , onde a posição é medida em metros e o tempo em segundos. Considere a direção na horizontal e na vertical.

(a) Determine os vetores posição e de cada partícula e o vetor posição relativa .

(b) Para ,faça um esquema no plano cartesiano dos vetores posição e e do vetor posição relativa . Determine a distância entre as partículas.

(c) Determine o(s) tempo(s) para o(s) qual(is) as duas partículas colidem.

(d) Determine a velocidade relativa, , no(s) instante(s) no(s) qual(is) as partículas colidem.