O gráfico abaixo mostra a aceleração de uma partícula como função do tempo:

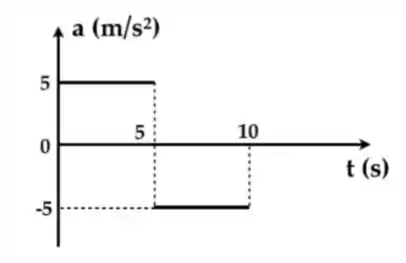
As figuras 1 a 4 abaixo mostram gráficos que podem representar a função posição , ou a velocidade , de uma dada partícula. Dentre as alternativas -, assinale a que corretamente associa os gráficos das figuras 1 a 4 à cinemática da partícula cuja aceleração é dada pelo gráfico acima.

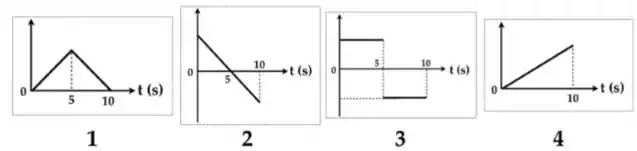
(a) As figuras 1 e 2 representam, respectivamente, a velocidade e posição da partícula como função do tempo.

(b) A figura 4 representa a posição da partícula como função do tempo.

(c) A figura 2 representa a velocidade da partícula como função do tempo.

(d) A figura 1 representa a velocidade da partícula como função do tempo.

(e) As figuras 3 e 4 representam, respectivamente, a velocidade e posição da partícula como função do tempo.

Vamos calcular primeiro as velocidades iniciais e finais da partícula para ter uma ideia de como é o gráfico. Utilizaremos a fórmula:

Para utilizar essa fórmula tem uma regra, a aceleração precisa ser constante! Então vamos ter que dividir nosso movimento em dois. Um com aceleração e outro com aceleração . Ficará assim:

Aceleração de :

O é apenas uma constante, vamos considerar que ele parta do repouso, ou seja,

Agora conseguirmos ver que a velocidade depende do tempo como uma equação de primeiro grau, ou seja, ela é uma reta. Como seu coeficiente é positivo, a reta é crescente.

Essa aceleração atua durante , então:

Aceleração de :

Nesse caso a aceleração de acontece quando termina a outra, então sua velocidade inicial é a velocidade final da primeira.

Novamente vemos que a velocidade depende do tempo como uma equação do primeiro grau, só que agora com coeficiente negativo. Portanto, é uma reta decrescente.

Como essa aceleração atua durante .

Vamos organizar agora o que aprendemos sobre a velocidade dessa partícula.

Nos primeiros ela é uma reta crescente que parte de até . E nos últimos ela é uma reta decrescente que parte de até .

Observando as figuras vemos que ela se parece mais com a figura número 1.