Cinemática Bidimensional, Movimento Relativo e Referencial
Duas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrita pelas funções posição , , e , onde a posição é medida em metros e o tempo em segundos. Considere a direção na horizontal e na vertical.
(a) Determine os vetores posição e de cada partícula e o vetor posição relativa .
(b) Para ,faça um esquema no plano cartesiano dos vetores posição e e do vetor posição relativa . Determine a distância entre as partículas.
(c) Determine o(s) tempo(s) para o(s) qual(is) as duas partículas colidem.
(d) Determine a velocidade relativa, , no(s) instante(s) no(s) qual(is) as partículas colidem.
Passo 1
Os vetores e são encontrados pela própria definição, onde a posição corresponde a componente , e a posição corresponde a componente .
Para a o ficará:
E para o fica:
Já o vetor posição relativa é obtido pela fórmula do movimento relativo:
Agora basta fazer a subtração de com e de com :
Passo 2
Substituindo para os vetores que encontramos no item anterior ficamos com:
Para representar estes vetores no plano cartesiano, basta indicar as coordenadas do ponto que encontramos para e desenhar uma seta da origem até o ponto.
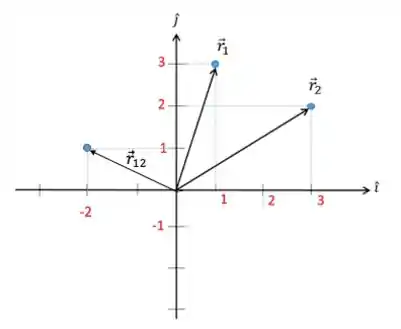
Agora só falta determinar a distância entre as partículas. Mas caramba, nós já temos isso! É o que posição relativa quer dizer. Posição relativa é a distância relativa às duas partículas.
Só que temos a distância relativa em forma de vetor, precisamos dar um valor para essa distância, que é justamente o comprimento desse vetor, ou seja, o módulo do vetor distância relativa. Basta utilizar a fórmula para encontrar o módulo de um vetor:
Lembrando que .
Passo 3
Vamos pensar. No item anterior nós descobrimos que a distância entre as partículas é o vetor posição relativa. E qual a distância entre as partículas quando elas colidem? Isso mesmo, se elas estão colidindo então a distância é zero. Logo, o vetor posição relativa tem que ser igual a zero.
Portanto, as duas componentes do vetor têm que ser iguais a zero.
e
Temos que para e , a primeira equação é satisfeita. No entanto, apenas para que a segunda equação é satisfeita. Daí, apenas para há colisão.
Passo 4
Lembrando que a velocidade nada mais é que a derivada do vetor posição. Basta derivarmos o vetor posição relativa, desta maneira:
Para derivar um vetor, basta derivar apenas as componentes:
Que resulta em:
Agora substituindo o instante que achamos para a colisão no item anterior, , temos:
Resposta
;
;