Um bloco de massa encontra-se sob um plano inclinado cuja superfície faz um ângulo com a horizontal. Nesta situação, o bloco encontra-se em repouso devido ao atrito estático com a superfície. A inclinação do plano é aumentada por um pequeno ângulo e o bloco começa a deslizar com aceleração de módulo igual a . Sobre os coeficientes de atrito cinético, , e estático, , para a força de atrito entre o bloco e a superfície do plano inclinado podemos afirmar:
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Vamos desenhar o sistema e as forças atuantes para entender melhor.
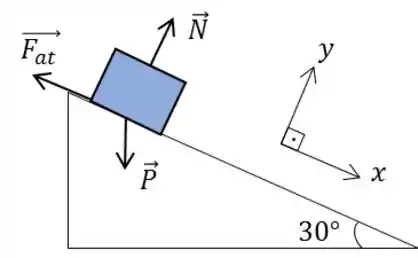
Agora, vamos decompor a força peso nos eixos e para ver enxergar melhor as coisas.
E também:
Passo 2
Certo. No primeiro momento o bloco está em equilíbrio pela força de atrito estática, logo todas as forças tem que se cancelar. Então:
Na vertical:
Na horizontal:
Essa é a estática, pois o bloco está em repouso.
Após inclinar um pouquinho de nada o plano inclinado, o bloco escorregou. Em outras palavras, isso quer dizer que o bloco estava na iminência de escorregar, que é o mesmo que dizer que ele estava prestes a escorregar, qualquer forcinha a mais aplicada na direção de iria fazê-lo escorregar.
Quando isso acontece, a força de atrito estática pode ser calculada pela fórmula:
Substituindo os valores que temos:
Aproximando :
Passo 3
Agora, em um segundo momento o bloco já não está mais em equilíbrio. Vamos aplicar a 2ª lei de Newton:
No eixo :
Substituindo os dados:
A força de atrito cinética é calculada pela fórmula:
O equilíbrio na vertical é mantido nesse segundo momento, logo a força normal continua tendo o mesmo valor, então, substituindo tudo:
Aproximando :
Resposta
Letra