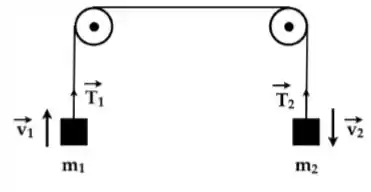
A figura abaixo mostra um esquema de polias ideais que sustentam os blocos e de massas e , respectivamente. Sabe-se que o bloco de massa movimenta-se para cima com velocidade constante. Sobre as grandezas físicas associadas a este sistema, podemos afirmar:

(a)

(b)

(c) e

(d)

(e)

Vamos analisar as opções uma a uma.

(a)

Errado! O enunciado nos diz que as polias são ideais. Por conta disso a tração em qualquer ponto da corta tem que ser a mesma. A polia ideal não pode mudar nada na corda exceto a direção e sentido da força.

(b)

Errado! O enunciado nos diz que o bloco sobe com velocidade constante, ou seja, não há aceleração! Aplicando a lei de newton ao bloco de massa ficamos com:

Como a aceleração é nula:

(c) e

Errada! Como os dois blocos estão ligados pelo fio, a aceleração dos dois são a mesma e já vimos no item anterior que essa aceleração é nula. Logo a parte que diz está correta.

Agora vamos aplicar a 2ª lei de Newton para o bloco de massa .

Mas já vimos que a aceleração é nula, então:

Entretanto, vimos no item que , logo:

E no item anterior vimos que . Então:

(d)

Errado. Assim como a aceleração é a mesma nos dois blocos, a velocidade também tem que ser a mesma nos dois blocos, pois eles estão conectados por um fio.

(e)

Correta! Como vimos no item , para que o conjunto se mova com velocidade constante (sem aceleração), os dois blocos precisam ter massas iguais.