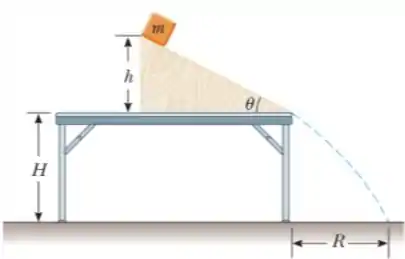
Um bloco de massa desliza sobre um plano inclinado que faz um ângulo com a horizontal. O plano tem uma superfície rugosa, cujo coeficiente de atrito cinético, , é igual a 0,2. O bloco localiza-se inicialmente no topo do plano, a uma altura com a horizontal, e inicia seu movimento a partir do repouso. O plano está montado sobre uma mesa de altura . Ao final do deslizamento ao longo do plano, o bloco cai sob ação da força peso e de uma força de resistência do ar. Veja a figura ao lado para um esquema da situação (use ).

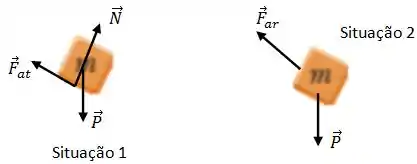
(a) Determine o diagrama de corpo livre (diagrama de forças) para o bloco quando o mesmo inicia seu movimento no topo do plano e outro diagrama para o bloco após o mesmo perder contato com o plano.

(b) Para cada força indicada nestes diagramas, aponte o devido par ação e reação (terceira Lei de Newton) da mesma e discuta seu efeito (escreva no máximo até duas linhas para cada força).

(c) Determine o vetor velocidade do bloco quando o mesmo atinge o final do plano inclinado. Escreva sua resposta na forma .

(d) Ignore a resistência do ar e determine o alcance do bloco. Dica geral: faça substituições numéricas apenas na etapa final das soluções dos itens (c) e (d). Para o item (d), caso você não tenha feito o item (c), deixe a resposta em termos de e .

(b)

Situação (1): força normal: força sobre a superfície do plano na direção , comprime o plano; força de atrito: força tangencial à superfície do plano na direção , arrasta a superfície do plano.

O plano não se desloca pois o supomos preso à mesa. Força peso: atração gravitacional do planeta Terra pelo bloco, atuando no centro do planeta Terra. Causa uma aceleração desprezível no planeta pois . (2) Força peso: mesma que anterior, força de resistência do ar: força sobre as partículas do ar, deslocando-as para passagem do bloco.

(c)

O bloco desce a rampa sobre a ação de forças constantes. Desta maneira, a resultante será uma força constante e movimento é uniformente acelerado. Adotamos um sistema de coordenadas e com denotando uma direção ao longo do plano e ao longo da normal ao plano. Podemos escrever, para uma coordenada ao longo da superfície do plano que:

Desta maneira, temos:

Uma vez que a aceleração é constante, conhecemos a equação de movimento para :

O deslocamento total em se escreve:

Onde é o tempo no qual o bloco está no fim do plano inclinado. Dái, escrevemos (lembrando que )

Mas o que queremos é a velocidade, que se escreve:

Desta maneira:

Colocando os números:

Uma opção alternativa para obter é usar a equação . Mas este é apenas o módulo da velocidade. Para encontrarmos o vetor velocidade na forma , adotamos o sistema de coordenadas usual e consideramos a geometria da figura. Desta maneira, escrevemos:

Desta maneira:

(d)

Sem resistência do ar, temos novamente um movimento a aceleração constante. De fato, escolhendo uma nova origem no “pé da mesa”, podemos escrever para o bloco (segunda lei de Newton):

ou seja,

Desta maneira:

Usando as condições do problema e nossa escolha de origem, temos:

Para determinar o alcance , primeiro calculamos o tempo de queda. Este é o tempo no qual , assim:

Resolvendo a equação, temos (tomando apenas a raiz positiva):

O alcance é dado pela equação: