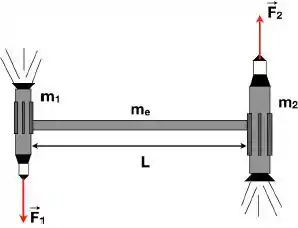
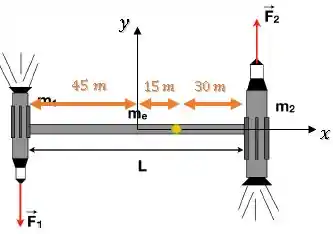
No espaço sideral, longe da influência gravitacional de qualquer planeta ou estrela, dois veículos espaciais munidos de fogutes estão acoplados a uma estação espacial longa de de comprimento. O sistema todo encontra-se em repouso. A massa de um dos veículos é e a do outro . A massa da estação espacial é e esta pode ser considerada como um cilindro delgado homogêneo. Os foguetes são acionados simultaneamente, de forma que a magnitude da força de reação dos gases de exaustão sobre cada veículos (i.e., o empuxo) é de e pode ser considerada perpendicular à estação espacial.
Importante: Quando necessário, faça substituições numéricas apenas nas expressões analíticas finais. Quantidades vetoriais devem ser expressas num sistema de coordenadas com uma base apropriada de versores.
Dados: (barra)
(a) Calcule a posição do centro de massa CM do sistema “veículos + estação espacial” com respeito à posição do centro de massa da estação espacial. Trate os veículos como massas pontuais.
(b) Escreva a equação de movimento para o CM do sistema do ítem (a) num referencial inercial antes e depois do acionamento dos foguetes. Que movimento descreve o CM após o acionamento?
(c) Determine o momento de inércia do sistema do ítem (a) com respeito a um eixo passando pelo seu CM e perpendicular ao plano de movimento dos veículos após o acionamento dos foguetes.
(d) Determine o vetor torque total com respeito ao CM devido ao empuxo dos foguetes.
(e) Calcule a magnitude da velocidade angular de rotação do sistema após o acionamento dos motores.
Passo 1
Na letra (a), queremos a posição do centro de massa desse sistema.
Primeiro de tudo, precisamos estabelecer um sistema de coordenadas que vamos usar ao longo de todo o exercício:
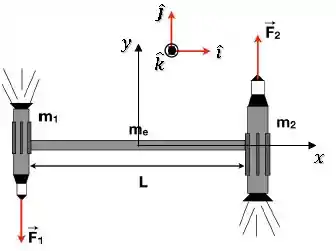
OBS: O eixo está para fora do papel.
Passo 2
O enunciado diz que podemos tratar dos dois foguetes como partículas.
Mas e a estação espacial?
Bom, para calcular a posição do centro de massa do sistema, vamos considerar a estação também como uma partícula em seu centro.
Como a estação é homogênia, o centro de massa desse corpo estará na origem.
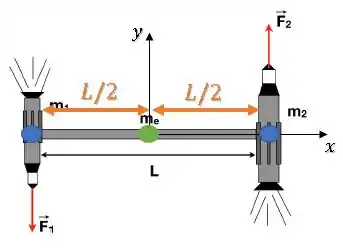
Assim, ficamos com:
Sabemos que o comprimento é de :
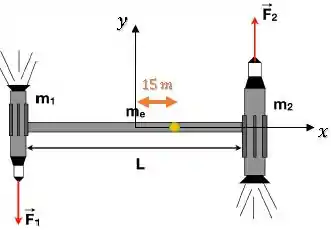
Ou seja, o CM está por aqui:
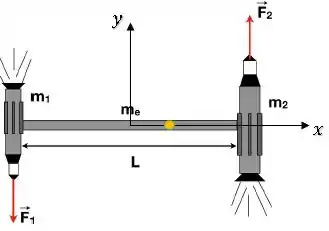
Podemos responder indicando a posição diretamente no eixo :
Ou então indicando o vetor posição :
Passo 3
Na letra (b), queremos a equação de movimento do centro de massa.
Para isso, vamos usar a segunda lei de Newton:
Antes do acionamento dos foguetes, não temos nenhuma força atuando sobre o sistema:
Enquanto depois do acionamento dos foguetes, temos:
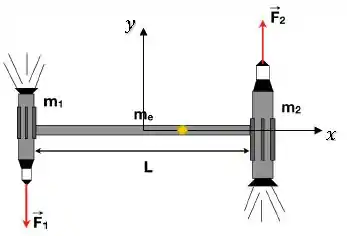
As duas forças são iguais a :
Assim, tanto antes quanto depois do acionamento dos foguetes, temos que a aceleração do centro de massa é nula:
Se não há aceleração, o centro de massa continua com a mesma velocidade, ou seja, em repouso.
Passo 4
Na letra (c), queremos o momento de inércia do sistema com relação ao eixo passando pelo CM.
O momento de inércia total será a soma do momento de inércia dos foguetes com o momento de inércia da estação (haste):
Passo 5
O momento de inércia de uma partícula é dado por:
Como consideramos os foguetes como partículas, temos:
Passo 6
Para calcular o momento de inércia da estação, vamos usar o valor o dado do enunciado de momento de inércia de uma barra:
Entretanto, esse valor é para um momento de inércia com relação a um eixo passando pelo centro de massa da barra (centro da barra).
Mas, estamos considerando um eixo de rotação que passa pelo centro de massa do sistema.
Então, vamos usar o Teorema dos eixos paralelos para calculá-lo.
A distância entre os eixos será:
Passo 7
Somando os momentos de inércia, temos:
Passo 8
Na letra (d), queremos o vetor torque resultante.
O torque resultante será a soma dos torques das forças de cada foguete.
O torque da força do foguete 1 será:
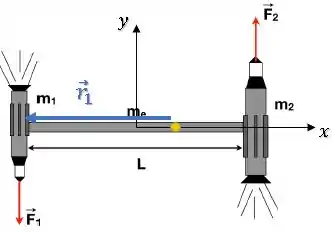
O produto vetorial de resulta em :
Já o torque da força do foguete 2 será:
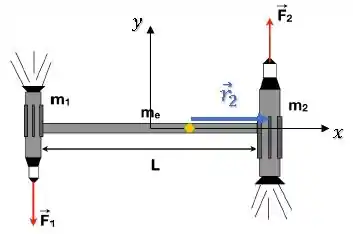
O produto vetorial de resulta em :
Então, o torque resultante é:
Passo 9
Na letra (e), queremos a velocidade angular após .
Pela segunda lei de Newton para rotações, temos que:
Passo 10
Como a aceleração angular é constante, podemos usar a equação de um MCA:
Como o sistema parte do repouso:
Substituindo os valores, temos:
Resposta
(a)
(b)
O centro de massa se mantem em repouso.
(c)
(d)
(e)