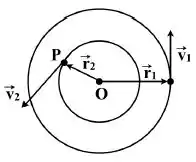
Um ponto material , com massa , esta amarrado com uma corda inextensível a uma haste vertical fina, posicionada no ponto O. A haste gira e produz uma trajetória circular do ponto , com raio inicial , velocidade inicial e velocidade angular . Após algum tempo, a corda foi envolta em torno da haste e o raio da própria trajetória é reduzido para um valor final . Podemos afirmar, em relacao às magnitudes da velocidade final () e da velocidade angular final () de , que:
(a) e
(b) a) e c) sao corretas
(c) Nenhuma é correta
(d) ,
(e) e
Passo 1
Nosso objetivo é comparar a velocidade e velocidade angular da partícula no momento inicial e final.
A única força que atua sobre a partícula é uma força de tração na corda:
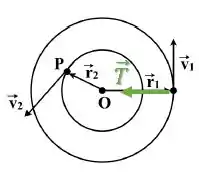
Como essa força aponta para o eixo de rotação (haste), ela não gera torque.
Se não há nenhum torque atuando sobre o sistema, o mmomento angular se conserva:
Podemos usar essa conservação para tirar as duas relações que precisamos.
Passo 2
O momento angular é dado pelo produto vetorial entre:
Como momento linear é dado por :
O movimento da partícula é aproximadamente circular, então esses dois vetores vão sempre ser perpendiculares:
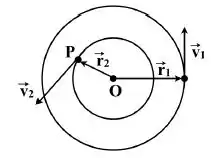
Ou seja o ângulo entre eles é de ...
O módulo daquele produto vetoria será:
Passo 3
Voltando para a conservação do momento angular, temos:
Ou seja, se o raio diminuiu de para , a velocidade deve aumentar de para afim de mante o produto dos dois constante.
Podemos observar assim também:
Como é maior que , temos que o termo:
Ou seja, a velocidade será maior que :
Passo 4
Mas e as velocidades angulares?
Bom, lembra que podemos relacionar a velocidade com a velocidade angular a partir de:
Aplicando essa relação na conservação de momento angular, temos:
Novamente, como é maior que , temos que o termo:
Ou seja, a velocidade será maior que :
Então, achamos que:
Ficamos com a letra (e).
Resposta
Letra (e)