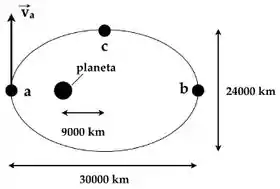
Um satélite segue a órbita elíptica da figura abaixo. A única força sobre o satélite é a atração gravitacional do planeta. A massa do satélite pode ser tomada como sendo completamente desprezível comparada àquela do planeta. A magnitude da velocidade do satélite no ponto a é . A magnitude da velocidade do satélite no ponto b é:
(a) impossível de determinar sem que as massas do planeta e do satélite sejam fornecidas.
(b) , já que o trabalho realizado pela força gravitacional sobre o satélite é nulo.
(c) , por conservação de momento linear do sistema satélite-planeta.
(d) , devido à conservação de momento angular do satélite.
(e) maior que , já que a velocidade angular do satélite é constante e .
Passo 1
Um ótimo jeito de comparar a velocidade nos pontos (mais próximo da trajetória) e (mais afastado da trajetória) é a partir da conservação do momento angular:
Bom, mas por que é útil utilizar o momento angular?
Porque ele relaciona a velocidade do satélite com a sua distância ao centro do planeta.
Mas por que o momento angular se conserva?
Ahh isso porque não há nenhum torque externo atuando no sistema:
A única força atuando nesse sistema é a força gravitacional. Como essa força sempre aponta na direção do centro de rotação, ela não gera torque.
Assim, temos a conservação do momento angular.
Passo 2
O momento angular é dado pelo produto vetorial entre o vetor posição e o vetor momento linear :
O momento linear e dado por :
Passo 3
Dá uma olhada nesses vetores:
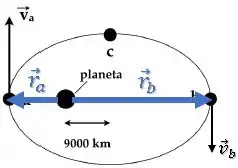
O módulo do produto vetorial entre eles é:
Onde é o ângulo entre eles.
Como nos dois casos os vetores são perpendiculares, temos:
Ou seja, o módulo do momento angular fica:
Passo 4
Voltando à conservação do momento angular, temos:
Passo 5
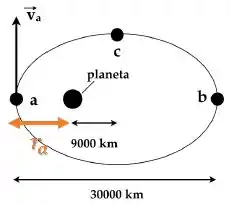
O semi-eixo maior da elipse é .
Podemos dizer que metade desse semi-eixo corresponde a:
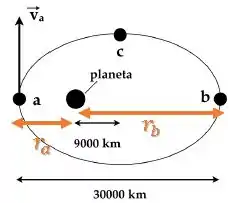
Passo 6
Substituindo os valores, temos:
OBS: Podemos substituir os valores de em em vez do , pois como fazemos o mesmo dos dois lados da equação, essas unidades se cancelam.
Resposta
Letra (d)