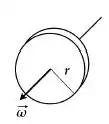
A figura mostra três discos homogêneos e feitos do mesmo material em rotação em torno de seus eixos de simetria. O ordenamento correto das energias rotacionais dos discos é:
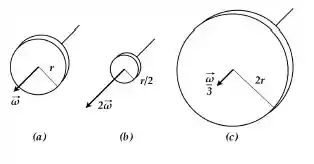
Dados: (cilindro)
(a)
(b)
(c)
(d)
(e)
Passo 1
A energia cinética de rotação é dada por:
Bom, já temos a velocidade angular em cada caso.
E o momento de inércia de um disco é o mesmo que de um cilindro (“vários discos”):
Então, basta substituir os valores do raio de cada um deles e calcular para cada caso, certo?
Não!!!

Temos que ter muito cuidado, pois o enunciado não disse que a massa dos discos são iguais!
Porémmm, sabemos que eles são homogêneos (massa uniformemente distribuída).
Então, suas massas serão proporcionais ao volume do disco.
Ou seja, quanto mais volume o disco tem, mais material ele tem, mais massa ele apresenta. Faz sentido né?
Passo 2
Vamos calcular o volume dos discos.
O volume de um disco é dado pela área da base:
vezes a altura do disco que chamaremos de .
Disco :
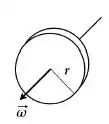
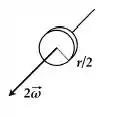
Disco :
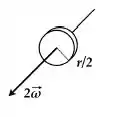
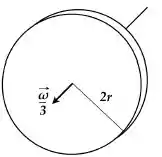
Disco :
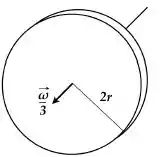
Passo 3
Podemos escrever a massa dos discos a partir da densidade (a mesma para todos):
Então, temos:
Passo 4
Agora que sabemos as massas, podemos descobrir os momentos de inércia de cada um deles, usando que:
Temos que:
Passo 5
Finalmente, podemos calcular a energia cinética de rotação de cada um:
Disco :
Disco :
Disco :
Podemos ver que todas as energias cinéticas têm uma constante multiplicada por um termo em comum.
Como:
Temos que:
Ficamos com a letra (d).
Resposta
Letra (d)