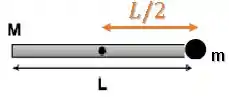
Uma haste, muito fina e homogênea, de massa e comprimento está inicialmente parada, suspensa por um fio que passa pela metade da barra (considere o fio inextensivel e de massa despreziavel). Um projétil de massa é lançado, com velocidade perpendicular à barra contra um dos seus extremos, de forma que o projétil permanece cravado na barra e o sistema começa a girar num plano perpendicular ao eixo do fio. Nestas condições, o módulo da velocidade angular () será dado por:
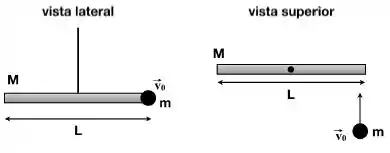
Dados: (barra)
(a)
(b)
(c)
(d)
(e)
Passo 1
Temos uma colisão entre uma partícula e uma haste e queremos saber a velocidade angular do sistema após a colisão.
Como não há nenhuma força externa exercendo um torque no sistema:
Temos que o momento angular do sistema se conserva:
OBS: Não é que não existem forças durante a colisão. Porém, a força que o projétil exerce sobre a haste é a mesma que a haste exerce sobre a bola só que com sentidos opostos... são forças internas ao sistema projétil+haste, por isso elas se cancelam assim como seus torques.
Passo 2
Beleza, mas porque usar a conservação de momento angular?
Se liga...
O momento angular de uma partícula (inicial) é dado por:
Sendo o vetor o vetor posição da partícula:
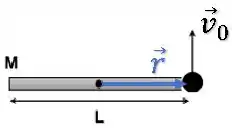
Como eles são perpendiculares, o módulo daquele produto vetorial fica assim:
Sendo que é igual a metade do comprimento da haste:
Após a colisão, temos que a haste e a partícula estão em rotação juntos.
O momento de inércia para um corpo extenso é calculado com:
Então, relacionando os momentos angulares, conseguimos achar a velocidade angular em função dos dados do problema:
Passo 3
Precisamos agora, calcular o momento de inércia do sistema haste+projétil após a colisão.
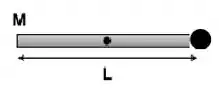
O momento de inércia total será a soma dos momentos de inércia da haste e do projétil:
Passo 4
O momento de inércia de uma haste fina com o eixo passando perpencidularmente pelo CM é:
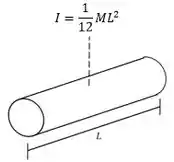
Logo temos:
Passo 5
Já o momento de inércia de uma partícula é dado por:
Onde é a distância da partícula ao eixo de rotação.
Logo, o momento de inércia do projétil é:
Achamos então que o momento de inércia total é:
Passo 6
Substituindo a expressão de na conservação de momento angular, temos:
Cancelando um dos dois lados:
Passo 7
Agora, para achar o resultado igual a uma das alternativas, damos uma olhada lá...
Nenhuma das respostas apresenta fração no denominador.
Então, vamos retirar aquelas frações colocando em evidência:
Ficamos com a letra (a).
Resposta
Letra (a)