P1 de Física 2 da UFRJ - 2019.2

A figura mostra o gráfico da pressão manométrica em função da profundidade para três fluidos em equilíbrio no campo gravitacional, suposto constante. Considere as seguintes afirmações:

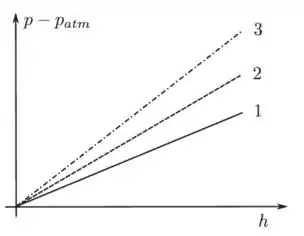
I. O empuxo sobre um mesmo corpo totalmente submerso é maior para o fluido 1.

II. Os três fluidos são incompressíveis.

III. Se colocarmos uma mesma massa M de cada fluido em recipientes idênticos, separados, a altura de fluido será a mesma em todos.

Marque a opção CORRETA.

(a) Somente a I está correta.

(b) Somente a II está correta.

(c) Somente a III está correta.

(d) Somente I e II estão corretas.

(e) Somente II e III estão corretas.

(f) Somente I e III estão corretas.

(g) Todas estão corretas.

(h) Nenhuma está correta.

Considere três esferas metálicas A, B e C de capacidades térmicas e inicialmente com temperaturas . A esfera A é posta em contato primeiramente com a esfera B até que se atinja o equilíbrio térmico. Após, a esfera A é afastada da esfera B e posta em contato com a esfera C até que se atinja novamente o equilíbrio térmico. Ao final desses procedimentos a temperatura da esfera A será:

(a)

(b)

(c)

(d)

A figura mostra três recipientes iguais, preenchidos pelo mesmo fluido incompressível até a mesma altura. Em dois deles patinhos diferentes estão flutuando. Marque a resposta que ordena corretamente os recipientes de acordo com o peso total P, em ordem decrescente:

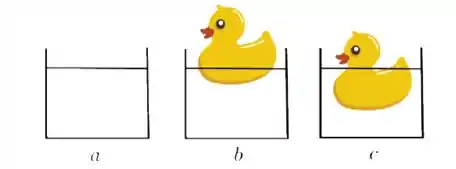
(a)

(b)

(c)

(d)

A figura mostra quatro recipientes preenchidos com o mesmo fluido incompressível, todos com um furo através do qual o fluido pode escoar. Todos são idênticos, mas o quarto tem um tubo conectado ao furo.

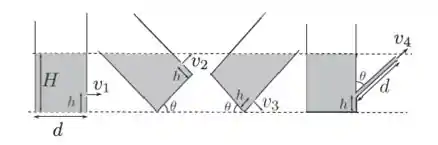
Considerando que a área da superfície livre do fluido é muito maior que a área do furo em todas as situações, e que todos os ângulos indicados são iguais a , marque a opção que indica a ordem correta do módulo da velocidade nos quatro casos.

(a) .

(b)

(c)

(d) .

(e)

Para qualquer temperatura a diferença entre os comprimentos de duas barras com coeficientes de expansão linear e é a mesma. Para que isto seja válido, a relação entre os respectivos comprimentos deve ser igual a:

(a)

(b)

(c)

(d)

O gráfico abaixo indica a temperatura da amostra de um dado material enquanto calor é fornecido a ela a uma taxa constante. Suponha que haja equilíbrio térmico em cada instante. Indique a ordem correta dos calores específicos e latentes de cada etapa indicada na figura.

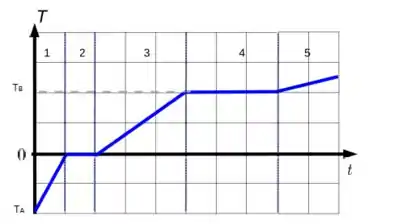
(a)

(b)

(c)

(d)

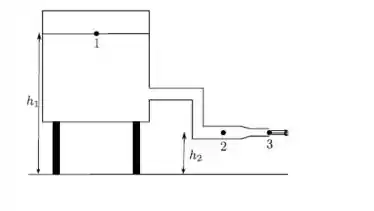
De um grande recipiente fechado para a atmosfera escoa água continuamente por um cano aberto, como podemos ver na figura. A altura do ponto 1 é e a dos pontos 2 e 3 é . A área transversal no ponto 2 e no ponto 3 é . A área transversal do recipiente é muito grande comparada com as áreas transversais do cano. Para simplificar, suponha e . A densidade da água é . Sabendo-se que num dado instante a velocidade do líquido no ponto 3 vale , calcule:

a) A pressão do ar retido na parte superior do reservatório.

b) A velocidade e a pressão no ponto 2.

c) A vazão volumétrica neste instante.

Um bloco cúbico de aresta a, feito de material homogêneo com densidade, está totalmente imerso em um fluido com densidade constante, em equilíbrio hidrostático e térmico à temperatura , como mostra a figura. Em seguida o conjunto é aquecido até atingir o equilíbrio na temperatura . Considerando que o coeficiente de dilatação volumétrica do fluido é e o coeficiente de dilatação volumétrica do bloco é , e que a aceleração da gravidade é uniforme com módulo , responda:

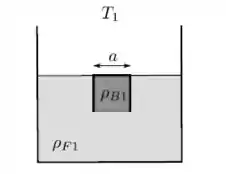
a) Obtenha a densidade do bloco em termos da densidade do fluido à temperatura .

b) Obtenha a densidade do fluido à temperatura .

c) Obtenha a densidade do bloco à temperatura .

d) Com base nos seus cálculos diga se, após a mudança de temperatura o bloco continuará flutuando totalmente submerso como na figura, apenas parcialmente submerso ou afundará totalmente, repousando sobre o fundo do recipiente. Justifique sua resposta.

Água escoa num fluxo estacionário numa tubulação horizontal tendo velocidade num ponto onde a área da seção transversal da tubulação vale . Num ponto onde a área da seção transversal se reduz a , temos para a vazão volumétrica e para a velocidade do líquido que:

(a) .

(b)

(c) .

(d) .

(e) .