Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Dilatação Térmica

Ver Teoria
Exercício 2612345678910111213141516171819202122232425272829303132333435

Enunciado

UFRJ- Física 2 – P1 2019.2

Um bloco cúbico de aresta a, feito de material homogêneo com densidade ρ B 1 , está totalmente imerso em um fluido com densidade constante ρ F 1 , em equilíbrio hidrostático e térmico à temperatura T 1 , como mostra a figura. Em seguida o conjunto é aquecido até atingir o equilíbrio na temperatura T 2 = 2 T 1 . Considerando que o coeficiente de dilatação volumétrica do fluido é β F e o coeficiente de dilatação volumétrica do bloco é β B < β F , e que a aceleração da gravidade é uniforme com módulo g , responda:

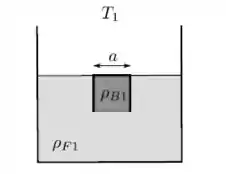
a) Obtenha a densidade do bloco em termos da densidade do fluido à temperatura T 1 .

b) Obtenha a densidade do fluido à temperatura T 2 .

c) Obtenha a densidade do bloco à temperatura T 2 .

d) Com base nos seus cálculos diga se, após a mudança de temperatura o bloco continuará flutuando totalmente submerso como na figura, apenas parcialmente submerso ou afundará totalmente, repousando sobre o fundo do recipiente. Justifique sua resposta.

Passo 1

  1. Na situação de T 1 temos um bloco imerso em fluido. E ele tá em equilíbrio hidrostático.

A palavra chave do enunciado para essa questão é equilíbrio! Isso porque quando ele fala isso ele nos diz que o módulo do peso do bloco é igual ao módulo do seu empuxo.

P b = E

m b g = ρ F 1 g V b

A massa do bloco pode ser escrita em termos de densidade. m b = ρ B 1 V b . Então

m b g = ρ F 1 g V b

ρ B 1 V b g = ρ F 1 g V b

Daí

ρ B 1 = ρ F 1

Prontinho!

Passo 2

b) Agora que o sistema foi aquecido temos que tanto o fluido quanto o bloco expandiram, como temos a mesma quantidade de matéria (a massa do fluido e do bloco não muda) que tínhamos antes, temos que a relação entre as densidades mudou, já que ρ = m V .

Então a densidade não vai ser mais a mesma coisa que antes. Como queremos a densidade do fluido, vamos ver como ocorreu a expansão volumétrica dele

V F 2 = V F 1 ( 1 + β F Δ T )

Mas

V F 2 = m F / ρ F 2

V F 1 = m F / ρ F 1

E Δ T = T 2 - T 1 = T 1

Então

m F / ρ F 2 = m F / ρ F 1 ( 1 + β F T 1 )

ρ F 1 ρ F 2 = ( 1 + β F T 1 )

Então

ρ F 2 = ρ F 1 1 + β F T 1

Maravilha!

Passo 3

c) Vai ser parecido com o ítem b. Mas agora é para o bloco. Então, analisando a expansão volumétrica do bloco:

V B 2 = V B 1 ( 1 + β B Δ T )

Do mesmo jeito que antes, temos que

V B 2 = m B / ρ B 2

V B 1 = m B / ρ B 1

E Δ T = T 2 - T 1 = T 1

Então

m B / ρ B 2 = m B / ρ B 1 ( 1 + β B T 1 )

ρ B 1 ρ B 2 = ( 1 + β B T 1 )

Então

ρ B 2 = ρ B 1 1 + β B T 1

Bem parecido com o do fluido. Beleza?

Passo 4

d) Eita.. ih agora?

Vamos pensar junto. O que faz um objeto flutuar e um fluido? Bom, a densidade do objeto tem que ser menor que a densidade do fluido. Pensa na agua e no gelo, por exemplo.

Então vamos analisar as densidades...

ρ B 2 = ρ B 1 1 + β B T 1

ρ F 2 = ρ F 1 1 + β F T 1

Calculando a razão entre elas:

ρ B 2 ρ F 2 = ρ B 1 1 + β B T 1   . 1 + β F T 1 ρ F 1

Como ρ B 1 = ρ F 1

ρ B 2 ρ F 2 = 1 + β F T 1 1 + β B T 1

Mas o enunciado nos diz que

β F > β B

Então o 1 + β F T 1 > 1 + β B T 1 . Logo 1 + β F T 1 1 + β B T 1 > 1 .

Então

ρ B 2 ρ F 2 > 1  

ρ B 2 > ρ F 2

Então o bloco não flutua. Ele afundará!

Resposta

a) ρ B 1 = ρ F 1

b) ρ F 2 = ρ F 1 1 + β F T 1

c) ρ B 2 = ρ B 1 1 + β B T 1

d) Afunda. Pois a densidade do bloco é maior do que a densidade do fluido.

Exercícios de Livros Relacionados

Determine a variação de volume de uma esfera de alumínio com um raio inicial de 10 c m quando a esfera é aquecida de 0 ° C para 100 ° C
A 20 ° C , uma barra tem exatamente 20,05 c m de comprimento, de acordo com uma régua de aço. Quando a barra e a régua são colocadas em um forno a 270 ° C , a barra passa a medir 20,11 c m de acordo c
Como resultado de um aumento de temperatura de 32 ° C , uma barra com rachadura no centro dobra pra cima . Se a distância fixa L 0 é 3,77 m e o coeficiente de dilatação linear da barra é 25.10 - 6 / °
Qual é o aumento de volume de um cubo de alumínio com 5,00c m de lado quando o cubo é aquecido de 10,0 ° C para 60,0 ° C ?
Três barras retilíneas de mesmo comprimento, feitas de alumínio, Invar e aço, todas a 20,0 ° C , formam um triângulo equilátero com pinos articulados nos vértices. A que temperatura o ângulo oposto à