Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pressão Hidrostática

Ver Teoria
Exercício 291234567891011121314151617181920212223242526272830313233

Enunciado

UFRJ- Física 2 – P1 2019.2

A figura mostra o gráfico da pressão manométrica em função da profundidade para três fluidos em equilíbrio no campo gravitacional, suposto constante. Considere as seguintes afirmações:

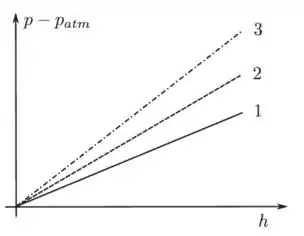
I. O empuxo sobre um mesmo corpo totalmente submerso é maior para o fluido 1.

II. Os três fluidos são incompressíveis.

III. Se colocarmos uma mesma massa M de cada fluido em recipientes idênticos, separados, a altura de fluido será a mesma em todos.

Marque a opção CORRETA.

(a) Somente a I está correta.

(b) Somente a II está correta.

(c) Somente a III está correta.

(d) Somente I e II estão corretas.

(e) Somente II e III estão corretas.

(f) Somente I e III estão corretas.

(g) Todas estão corretas.

(h) Nenhuma está correta.

Passo 1

Vamos lá. Analisando cada alternativa.

Primeiro: I. O empuxo sobre um mesmo corpo totalmente submerso é maior para o fluido 1.

Temos um gráfico de p - p a t m . A pressão é dada por

p = p a t m + ρ g h

Então

p - p a t m = ρ g h

E o empuxo é dado por

E = ρ g V

Daí:

ρ g = E V

Vamos substituir isso lá na equação da pressão:

p - p a t m = E V h

Notem que E   e p - p a t m são proporcionais. Então, quanto maior E maior p - p a t m . Como o fluido 3 tem o maior p - p a t m , então ele tem o maior empuxo.

Logo, essa tá errada!

Passo 2

II. Os três fluidos são incompressíveis.

Pela equação que vimos antes:

p - p a t m = ρ g h

E olhando para o gráfico da figura, p - p a t m v s .   h temos que é um gráfico de uma reta, cujo coeficiente angular é ρ g , que deve ser constante, pois é uma reta. Ela deve ter a mesma inclinação sempre em relação à horizontal. Como g   é uma constante, temos que ρ também deve ser constante. Quando a densidade é constante o fluido é incompressível.

Essa tá certinha!

Passo 3

III. Se colocarmos uma mesma massa M de cada fluido em recipientes idênticos, separados, a altura de fluido será a mesma em todos.

A massa de cada fluido pode ser escrita como

M = ρ 1 V 1

M = ρ 2 V 2

M = ρ 3 V 3

Daí

ρ 1 V 1 = ρ 2 V 2 = ρ 3 V 3

Se os recipientes forem idênticos, então a área transversal também será igual para todos. Podeos escrever o volume de cada fluido como A h 1 ,   A h 2 e A h 3 .

ρ 1 V 1 = ρ 2 V 2 = ρ 3 V 3

ρ 1 A h 1 = ρ 2 A h 2 = ρ 3 A h 3

As densidades são diferentes porque cada reta tem uma inclinação diferente. Então as alturas também devem ser diferentes de forma que a igualdade seja mantida.

ρ 1 h 1 = ρ 2 h 2 = ρ 3 h 3

Elas vão se balancear e o produto delas será igual.

Resposta

Letra b)

Exercícios de Livros Relacionados

Em uma girafa, com a cabeça 2,0m acima do coração e o coração 2,0m acima do solo, a pressão manométrica (hidrostática) do sangue na altura do coração é 250t o r r . Suponha que a girafa está de pé e a
Alguns membros de uma tripulação tentam escapar de um submarino avariado 100m abaixo da superfície. Que força deve ser aplicada a uma escotilha, de 1,20m ×0,6m , para empurrá-la para fora a essa profu
Um grande aquário de 5 m de altura está cheio de água doce até uma altura de 2 m . Uma das paredes do aquário é feita de plástico e tem 8,00m de largura. De quanto aumenta a força exercida sobre a par
(Embolia gasosa em viagens de avião) Os mergulhadores são aconselhados a não viajar de avião nas primeiras 24 horas após um mergulho, porque o ar pressurizado usado durante o mergulho pode introduzir
Na Fig. 14-35, a água atinge uma altura D=35,0m atrás da face vertical de uma represa com W = 314m de largura. Determine (a} a força horizontal a que está submetida a represa por causa da pressão mano