Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 88123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687899091929394

Enunciado

UFRJ- Física 2 – P1 2019.2

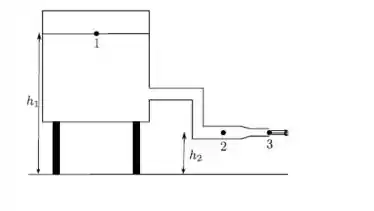
De um grande recipiente fechado para a atmosfera escoa água continuamente por um cano aberto, como podemos ver na figura. A altura do ponto 1 é h 1 = 10   m   e a dos pontos 2 e 3 é h 2 = 2   m . A área transversal no ponto 2 é   A 2 = 0 ,   048   m 2   e no ponto 3 é A 3 = 0 ,   024   m 2 . A área transversal do recipiente é muito grande comparada com as áreas transversais do cano. Para simplificar, suponha 1   a t m = 10 5   N / m 2 e g = 10   m / s 2 . A densidade da água é 10 3   k g / m 3 . Sabendo-se que num dado instante a velocidade do líquido no ponto 3 vale v 3 = 10   m / s , calcule:

a) A pressão p 1 do ar retido na parte superior do reservatório.

b) A velocidade v 2 e a pressão p 2 no ponto 2.

c) A vazão volumétrica neste instante.

Passo 1

Temos um fluido em movimento. Então considerando que tá tudo bonito (escoamento estacionário e o fluido seja incompressível tem uma linha de corrente que liga 1 e 3) podemos aplicar a equação de Bernoulli.

P 1 + ρ g h 1 + 1 2 ρ v 1 2 = P 3 + ρ g h 2 + 1 2 ρ v 3 2

P 1 é o que queremos saber.

P 1 = P 3 + ρ g h 2 - h 1 + 1 2 ρ ( v 3 2 - v 1 2 )

P 3 é a pressão atmosférica. h 1 = 10 m e h 2 = 2   m . A densidade vale 10 3   k g / m 3 .

A área do recipiente é muito maior do que a área do cano, ou seja, A 1 ≫ A 3 , dessa forma, podemos desconsiderar a velocidade do ponto 1. Já que pela equação da continuidade temos A 1 v 1 = A 3 v 3 Beleza?

Substituindo os dados:

P 1 = 10 5 +   10 3 ( 10 ) 2 - 10 + 1 2 10 3 ( 10 2 - 0 )

P 1 = 10 5 +   10 3 ( 10 ) - 8 + 1 2 10 3 ( 10 2 )

P 1 = 70000   P a = 0,7 a t m

Passo 2

b)

Primeiro, vamos achar a velocidade. Usando a lei da continuidade:

A 2 v 2 = A 3 v 3

0 ,   048   v 2 = 0,024   10

v 2 = 5   m / s

Show!

E para encontrarmos a pressão, vai ser parecido com o que fizemos antes, mas vamos aplicar a equação de Bernoulli entre os pontos 2 e 3.

P 2 + ρ g h 2 + 1 2 ρ v 2 2 = P 3 + ρ g h 2 + 1 2 ρ v 3 2

As alturas são iguais, portanto os termos ρ g h 2 vão se anular. E vamos substituir os dados.

P 2 = P 3 + 1 2 ρ v 3 2 - v 2 2

P 2 = 10 5   + 1 2 ( 10 3 ) 10 2 - 5 2

P 2 = 10 5   + 3,75 × 10 4

P 2 = 137500   P a = 1,375   a t m

Passo 3

c)

A vazão volumétrica é o quanto de volume de fluido passa por tempo em um pedação do tubo.

No instante em que a velocidade 3 vale 10 m / s , temos:

R = A 3 v 3

R = ( 0,024 ) 10

R = 0,24   m 3 / s

Prontinho.

Resposta

a) 0,7 a t m

b) P 2 = 137500   P a = 1,375   a t m

c) R = 0,24   m 3 / s

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d