UFRJ- Física 2 – P1 2019.2
Água escoa num fluxo estacionário numa tubulação horizontal tendo velocidade num ponto onde a área da seção transversal da tubulação vale . Num ponto onde a área da seção transversal se reduz a , temos para a vazão volumétrica e para a velocidade do líquido que:
(a) .
(b)
(c) .
(d) .
(e) .
Passo 1
Bom, o tubo é o mesmo. Ele só afinou na região 2. Mas a quantidade de fluido que passava no ponto 1 em um intervalo de tempo tem que passar no ponto 2 também, porque o que entra tem que sair!
Pelo principio da continuidade, temos:
Substituindo os dados:
Show!
Passo 2
E agora vamos pra vazão. Mas o que isso quer dizer? Isso é a quantidade de volume de fluido que está passando por unidade de tempo.
Agora, pensa aqui comigo. O volume de fluido que temos ali nessa região do desenho é :
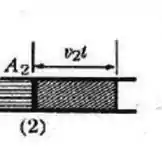
Isto é, o volume é a área do tubo vezes a “altura”, que escrevemos em termos de velocidade.
Então a vazão volumétrica é:
Então
Tranquilo?
Resposta
Letra a)