P2 de Física 2 da UFRJ - 2015.1

Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA:

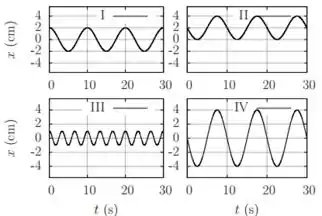
1. Todos, exceto oscilam com período de
2. e partem de sua posição de equilíbrio em
3. e oscilam com a mesma amplitude.
4. oscila com frequência menor que todos os restantes,
5. realiza oscilações por minuto.

Considere uma onda dada por que atinge a extremidade de uma corda, fixa em Neste caso, qual é a forma da onda refletida?

Um oscilador harmônico amortecido de frequência natural de oscilação , oscila sujeito a uma força externa periódica, da forma .Seu deslocamento em função do tempo durante dois minutos é exibido no gráfico abaixo. Julgue as afirmativas:

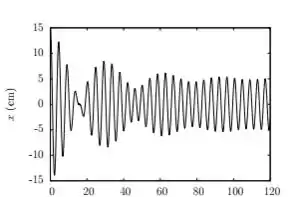
- O fenômeno de batimentos observado para indica a sobreposição de frequências diferentes. No entanto, uma das frequências é gradualmente atenuada pelo amortecimento.

- Após um intervalo de tempo suficientemente longo, o oscilador oscilará de forma periódica, com período:

- A partir de as forças de amortecimento cessam de agir no sistema.

- Em seu regime estacionário, a média de energia mecânica do oscilador sobre uma oscilação é conservada. No entanto, o mesmo não é verdade para a energia a cada instante.

1. Apenas e estão corretas.
2. Apenas e estão corretas.
3. Apenas a esta incorreta.
4. Apenas a esta incorreta.

Considere uma corda feita de um material homogêneo. Qual das afirmativas a seguir está INCORRETA?

1. Uma onda refletida em uma extremidade tem sempre uma frequência idêntica à onda incidente.
2. A soma de uma onda totalmente refletida por uma extremidade e da onda incidente formará sempre uma onda estacionária
3. Duas condições de contorno são suficientes para que o número de onda seja quantificado.
4. Não há propagação de energia ou de momento numa onda estacionária.
5. Uma quantificação do numero de onda não implica numa quantificação da frequência angular.

Considere duas molas, a mola 1 tem frequência natural enquanto a mola 2 tem frequência natural Ambas estão sob a ação de uma mesma força externa periódica que oscila com frequência A respeito da solução particular de ambas, podemos afirmar que:

1. Ambas oscilam em fase com a mesma frequência e mesma amplitude.
2. As molas oscilam defasadas mas com mesma frequência e mesma amplitude.
3. As molas oscilam em fase com mesma frequência e 2 apresenta uma amplitude maior que 1
4. A mola 2 oscila com maior amplitude e frequência que 1. Elas podem estar ou não em fase, dependendo das condições iniciais.
5. As molas oscilam fora de fase com mesma frequência e 2 apresenta uma amplitude maior do que 1.

Um bloco de massa oscila preso a uma mola, de constante e comprimento natural na presença de um vento, cujo o efeito pode ser modelado como uma força constante:

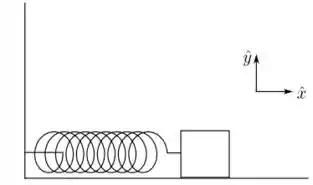
1. Escolha um sistema de coordenadas pra descrever esse movimento e diga onde está a origem. Usando esse sistema, obtenha a posição de equilíbrio do bloco.
2. Escreva a equação diferencial desse movimento supondo que não haja nenhum amortecimento.
3. Escreva a solução geral da equação acima para o caso
4. Escreva a função que descreve o movimento deste bloco , para , supondo que em a mola está com o comprimento natural e o bloco em repouso.

A figura abaixo representa o perfil de uma corda vibrante de de comprimento em instantes de tempo diferentes. Considere que a corda satisfaz a equação de corda vibrante, onde o deslocamento transversal é dado como função da posição e do tempo

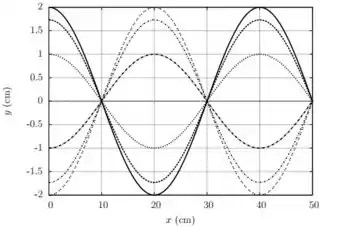
1. Sabendo que o deslocamento nunca ultrapassa , determine os parâmetros , o comprimento de onda a partir do gráfico acima.
2. A partir da equação de onda e sabendo que a frequência angular de vibração é , encontre a velocidade de propagação das ondas na corda.
3. Que condições de contorno pra e podem gerar esta onda como um modo normal de vibração? O que pode ser dito sobre as extremidades da corda neste caso?
4. Quais os outros valores do comprimento de onda que geram modos normais satisfazendo essas condições? Explique seu raciocínio.

Marque a afirmação INCORRETA a respeito do comportamento da oscilação de uma corda. Aqui, são frequência angular, número de onda, comprimento de onda e período, respectivamente.

1. A velocidade da onda aumenta se a densidade linear da corda diminuir.
2. A frequência é proporcional a
3. A densidade de energia é proporcional à amplitude.
4. A velocidade da fase é dada por .
5. A velocidade da fase é dada por

Uma fonte sonora em repouso faz-se ouvir por dois observadores, e ,também em repouso. A partir de um certo momento, esta fonte começa a se mover com velocidade constante. A figura abaixo mostra e e as frentes de ondas produzidas por em repouso, à esquerda, e em movimento, à direita. Sobre a segunda situação, assinale a alternativa CORRETA:

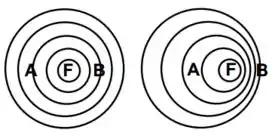
1. A fonte se move pra esquerda.
2. O período de onda parece maior para
3. e observam o mesmo comprimento de onda.
4. A velocidade de propagação das ondas depende da direção de observação.
5. observará um comprimento de onda maior que

Marque a opção que NÃO representa uma solução da equação de onda para uma corda. Considere que as constantes e são todas diferentes de zero: