Um bloco de massa oscila preso a uma mola, de constante e comprimento natural na presença de um vento, cujo o efeito pode ser modelado como uma força constante:
![]()
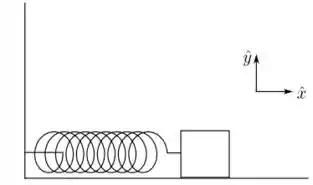
- Escolha um sistema de coordenadas pra descrever esse movimento e diga onde está a origem. Usando esse sistema, obtenha a posição de equilíbrio do bloco.
- Escreva a equação diferencial desse movimento supondo que não haja nenhum amortecimento.
- Escreva a solução geral da equação acima para o caso
- Escreva a função que descreve o movimento deste bloco , para , supondo que em a mola está com o comprimento natural e o bloco em repouso.
Passo 1
a):
Bom, vamos chamar de a posição na qual a mola fica com o seu comprimento inicial . Assim:
Agora vamos considerar sendo essa a origem do novo sistema de coordenadas. Assim, os valores de pra esse novo sistema são:
Onde é referente ao antigo sistema. Show? Bom, só que aquilo ali encima é a elongação de uma mola. Então a força elástica pode ser escrita assim:
Show!
E como achar a posição de equilíbrio,
É só igualar os módulos das forças que atuam no bloco. Ou seja:
Mas qual o sinal que vamos por ali? Bem, como a força aponta na direção negativa de , graças ao sinal que está na frente da força, é de se esperar que a posição de esteja antes do comprimento natural da mola, isso é, da nova origem.
Como vai estar antes da origem, vai ser negativo:
Passo 2
b):
Vamos tirar a equação diferencial a partir da segunda Lei de Newton:
Passo 3
c):
Para o caso , a equação diferencial vira uma EDO homogênea:
Então, a solução vai ser a solução de um MHS:
Passo 4
d):
Bom, se você lembrar de Cálculo 2, vai saber que essa equação diferencial é uma EDO não homogênea. Então, a solução é dada por:
Bom, a solução da equação homogênea é dada pelo item anterior:
E a solução particular a gente acha assim:
Damos um chute pra . Como a força é constante, a solução também:
Então:
Então a solução é dada por:
Precisamos achar E . Usando as condições:
Então:
E:
Beleza, já sabemos que a fase é um múltiplo inteiro de
Só que, como e são positivos:
Então:
Então:
Assim:
Resposta
a):
b):
c):
d):