Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA:
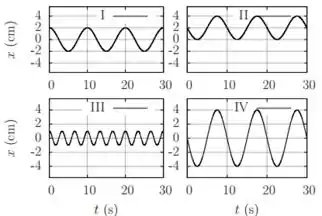
- Todos, exceto oscilam com período de
- e partem de sua posição de equilíbrio em
- e oscilam com a mesma amplitude.
- oscila com frequência menor que todos os restantes,
- realiza oscilações por minuto.
Passo 1
Bom galera, o macete aqui é tentar comparar o período e a frequência de cada MHS.
Lembrando que: Período é o tempo necessário para que um ciclo seja realizado, e frequência é o número de oscilações por segundo.
Passo 2
Então, de cara, qual é o movimento que tem mais oscilações por segundo, ou seja, maior frequência?
É só a gente comparar quantas “ondinhas” cada MHS tem, num mesmo espaço de tempo.
Sacou?
Bom, se você entendeu certinho, percebeu que é o que tem a maior frequência.(:
Passo 3
Logo, como a d) nega isso, ela é a INCORRETA:d)
Ok!!! Mas vamos analisar as outras alternativas??? ![]()
Passo 4
- Todos, exceto oscilam com período de
Ao analisarmos os períodos dos quatro osciladores, podemos perceber os seguintes períodos:
- -
- -
- -
- –
Logo, afirmação CORRETA.
As posições de equilíbrio de e são as posições em torno das quais eles oscilam. Essas posições são para o oscilador e para o oscilador . Dessa forma, percebemos que essa afirmação está CORRETA.
A amplitude do movimento é a diferença entre o máximo valor da variável e a sua posição de equilíbrio. Desta forma, percebemos que as amplitudes de e são equivalentes e iguais a . Afirmação CORRETA.
- realiza oscilações por minuto.
Percebemos que o oscilador realiza 9 oscilações em 30 segundos. Logo, em 60 segundos (1 minuto) ele realizará 18 oscilações. Afirmação CORRETA.
Resposta
d)