A figura abaixo representa o perfil de uma corda vibrante de de comprimento em instantes de tempo diferentes. Considere que a corda satisfaz a equação de corda vibrante, onde o deslocamento transversal é dado como função da posição e do tempo
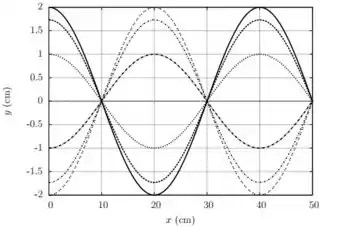
- Sabendo que o deslocamento nunca ultrapassa , determine os parâmetros , o comprimento de onda a partir do gráfico acima.
- A partir da equação de onda e sabendo que a frequência angular de vibração é , encontre a velocidade de propagação das ondas na corda.
- Que condições de contorno pra e podem gerar esta onda como um modo normal de vibração? O que pode ser dito sobre as extremidades da corda neste caso?
- Quais os outros valores do comprimento de onda que geram modos normais satisfazendo essas condições? Explique seu raciocínio.
Passo 1
a):
Bom galera, pra achar a amplitude a partir do gráfico, basta a gente olhar pro maior valor que pode atingir. Esse valor é:
Também a partir do gráfico, percebemos que:
Com o valor do comprimento fica fácil calcular o número de onda:
Resta saber a fase . Bom, pra isso, vamos pegar o valor de quando
Assim:
Onde:
Mas como você pode ver no gráfico, não existe um nó em . Então a fase não pode ser , pois:
E como os valores de em atingem um máximo, tanto positivo quanto negativo, a fase tem que ser um múltiplo inteiro de
Passo 2
b):
Bom, ela nos obriga a usar a equação de onda. Então vamos lá:
Vamos então, derivar duas vezes em relação à e duas vezes em relação a primeiro:
Duas vezes em relação a
Duas vezes em relação ao tempo:
Agora, vamos mexer um pouco na equação de onda pra isolar o
E chegamos na velha relação:
Então:
Passo 3
c):
Bom, basicamente a questão está querendo saber se nas extremidades terão nós ou ventres. Quando uma questão te pede as condições de contorno em uma onda estacionaria, geralmente é isso.
Bom, como você pode ver na figura, existe um nó na extremidade direita e um ventre na esquerda, pra esse modo de oscilação da figura.
Então, pro modo normal, vai ser a mesma coisa: um ventre na extremidade esquerda, em e um nó na extremidade direita,
Mas como escrever isso matematicamente?
A condição pra extremidade direita é fácil, é só atribuir a todo valor de
E o da esquerda?
Bom, ali é um ventre. E o que acontece com a derivada parcial da função em relação à em um ventre? Ela dá zero!
Por que? Bom, como o gráfico da questão é , a derivada parcial em relação a vai dá o coeficiente da reta tangente ao gráfico no ponto
E como um ventre é um máximo, a reta tangente vai ser horizontal....logo, com coeficiente igual a zero.
Então:
São essas duas condições.
E o que pode ser dito em relação as extremidades é que existe um nó na extremidade direita e um ventre na esquerda, pra esse modo de oscilação da figura.
Passo 4
d):
Bom, olhando pra figura, você vai ver que a soma das frações de comprimento de ondas dão:
Como pra satisfazer as condições de contorno a gente sempre vai ter um ventre numa ponta e um nó na outra. Então, vamos ter sempre uma relação do tipo:
Onde é um numero impar. Reescrevendo isso:
Que é igual a relação necessária pra que se tenha um tubo sonora fechado, como vamos ver no capítulo de som.
Enfim, a relação pode ser escrita assim:
Resposta
a):
b):
c):
d):