Um oscilador harmônico amortecido de frequência natural de oscilação , oscila sujeito a uma força externa periódica, da forma .Seu deslocamento em função do tempo durante dois minutos é exibido no gráfico abaixo. Julgue as afirmativas:
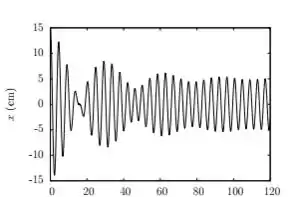
- O fenômeno de batimentos observado para indica a sobreposição de frequências diferentes. No entanto, uma das frequências é gradualmente atenuada pelo amortecimento.
- Após um intervalo de tempo suficientemente longo, o oscilador oscilará de forma periódica, com período:
- A partir de as forças de amortecimento cessam de agir no sistema.
- Em seu regime estacionário, a média de energia mecânica do oscilador sobre uma oscilação é conservada. No entanto, o mesmo não é verdade para a energia a cada instante.
- Apenas e estão corretas.
- Apenas e estão corretas.
- Apenas a esta incorreta.
- Apenas a esta incorreta.
Passo 1
Vamos julgar uma por uma:
- Verdade! Bem, a figura realmente representa um batimento, certo? Além disso, nós sabemos que no regime estacionário, o sistema oscila com a frequência da força externa.
No entanto, o sistema possui a sua frequência padrão, que é o , e no inicio, oscila com essa frequência. Então, a frequência angular do batimento será:
E a frequência linear será:
- Pegando carona na explicação anterior: Verdade! Por que? Porque no regime estacionário, o sistema passa a oscilar com a frequência da força externa, . Então, o período será:
Passo 2
-Falsa! As forças de amortecimento não deixam de agir no sistema. Isso nunca foi dito, o que acontece é que a oscilação passa a ser dominada pela força externa.
As forças de amortecimento, que são forças de atrito, dissipam a energia do sistema, certo?
O que acontece no regime estacionário é que a força externa repõe essa energia perdida. Isso faz com que a amplitude da oscilação no regime estacionário se mantenha constante, mas as forças de atrito continuam ali sim.
-Verdadeira- Essa pergunta é um pouco complicada. Bem, sabemos que no regime estacionário o sistema vai oscilar com uma frequência , e com uma amplitude constante dada pela fórmula:
Além disso, o movimento no regime permanente é um MHS. Assim, a energia mecânica seria dada por:
Beleza, mas não existem forças dissipativas? Quando existem forças dissipativas num sistema, a energia mecânica não se conserva, não é mesmo?
Sim, por isso eu pego carona na explicação anterior. Como existem forças dissipativas dissipando energia a cada instante, se olhássemos pro sistema num espaço de tempo muito pequeno, um , veríamos um sistema não conservativo.
No entanto, olharmos um longo espaço de tempo , veremos um sistema cuja energia mecânica se conserva graças às reposições de energia que são feitas pela força externa. Sacou? Assim, a média vai ser próxima do valor:
Resposta
c)