P3 de Física 2 da UFRJ - 2020.2

Qual destas mudanças podemos fazer em um movimento harmônico simples para dobrar a velocidade máxima do movimento?

Escolha uma opção:

Quadruplicar a energia

Quadruplicar a amplitude

Quadruplicar o período

Multiplicar a energia por .

Duplicar o período.

A respeito de um oscilador harmônico sujeito a uma força externa harmônica, podemos afirmar que:

Escolha uma opção:

A energia mecânica do oscilador é sempre constante

O oscilador sempre se moverá com a sua frequência angular natural, independente da força externa.

A amplitude do movimento do oscilador é independente da sua massa.

Se não houver amortecimento, a amplitude do movimento do oscilador tende a infinito quando a frequência da força externa tende a frequência natural do oscilador.

Se houver amortecimento, a amplitude do movimento do oscilador é sempre constante com o tempo.

Seja a equação diferencial que descreve um oscilador harmônico amortecido. Considere as situações: , e . Esses regimes correspondem, respectivamente, aos casos:

Escolha uma opção:

crítico, supercrítico e subcrítico.

crítico, subcrítico e supercrítico.

supercrítico, subcrítico e crítico.

subcrítico, subcrítico e crítico.

subcrítico, crítico e supercrítico.

subcrítico, supercrítico e crítico.

Um objeto massivo é preso a uma mola tal que a sua função movimento pode ser obtida como solução da equação diferencial , onde é uma constante real positiva. Sabe-se que, em , ele se encontra na posição de equilíbrio e sofre um impulso tal que sua velocidade inicial é . É correto afirmar que:

Escolha uma opção:

A posição deste objeto oscila em torno da posição de equilíbrio com amplitude inicial e decrescente com o tempo.

O maior deslocamento alcançado por este objeto é .

Este sistema representa um oscilador harmônico amortecido; logo a solução é sempre decrescente (em módulo).

Este sistema representa um oscilador harmônico amortecido e, como o objeto já está inicialmente na posição de equilíbrio, ele não se move.

O maior deslocamento alcançado por este objeto é .

Considere uma caixa de madeira de massa , inicialmente em equilíbrio sobre uma superfície horizontal (sem atrito), ligada a uma mola ideal de constante presa a uma parede. No instante um projétil de massa e velocidade em módulo, se movendo na direção horizontal, atinge a caixa e fica preso a ela. Após isto, o sistema formado pela caixa e pelo projétil passa a oscilar harmonicamente. A frequência angular e a velocidade inicial do sistema são dadas, respectivamente, por

Escolha uma opção:

e

e

e

e

e

A frequência angular de um oscilador amortecido no regime sub-crítico é . Caso não houvesse o amortecimento, esse valor seria Qual o valor da constante de amortecimento , caso ? Considere conhecida a massa do sistema .

Escolha uma opção:

Considere o gráfico abaixo, que representa a posição de um oscilador harmônico simples.

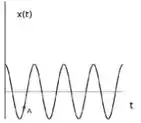
Quando o sistema encontra-se no ponto , podemos afirmar que:

Escolha uma opção:

A posição e a velocidade são ambas negativas e a aceleração é positiva.

A posição e a velocidade são ambas positivas e a aceleração é positiva.

A posição é positiva, a velocidade é negativa e a aceleração é nula, pois é um ponto de inflexão da curva.

A posição é positiva, a velocidade é nula e a aceleração é negativa.

A posição é negativa e a velocidade e a aceleração são positivas.

A solução geral para uma partícula realizando um movimento harmônico simples pode ser escrita como: . Considerando que no instante a posição da partícula vale e sua velocidade é positiva, qual é o valor da constante de fase?

Escolha uma opção:

. Uma mola uniforme, cujo comprimento sem distensão é , tem constante elástica . A mola é cortada em duas partes iguais de comprimento sem distensão cada uma. Qual o valor da constante elástica de cada um destes dois pedaços de mola?

Escolha uma: