Considere o gráfico abaixo, que representa a posição de um oscilador harmônico simples.
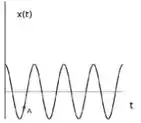
Quando o sistema encontra-se no ponto , podemos afirmar que:
Escolha uma opção:
A posição e a velocidade são ambas negativas e a aceleração é positiva.
A posição e a velocidade são ambas positivas e a aceleração é positiva.
A posição é positiva, a velocidade é negativa e a aceleração é nula, pois é um ponto de inflexão da curva.
A posição é positiva, a velocidade é nula e a aceleração é negativa.
A posição é negativa e a velocidade e a aceleração são positivas.
Passo 1
Observando bem o gráfico de já podemos tirar algumas informações para eliminar alguns itens.
O ponto está em uma posição negativa no gráfico e só com isso já podemos eliminar os itens , e .
Outra coisa importante é que a derivada é a inclinação da reta tangente no ponto então podemos ver que no ponto a derivada é positiva, assim podemos excluir a letra e o que sobra é a letra .
Então por eliminação temos que a letra é a alternativa correta.
Resposta
A posição é negativa e a velocidade e a aceleração são positivas.