Um bloco de massa está preso à extremidade inferior de uma mola ideal de constante elástica cujo extremo superior está preso ao teto por um suporte fixo e alinhada com a direção vertical. Um segundo bloco, também de massa , está ligado ao primeiro bloco por meio de um fio ideal. Inicialmente, o sistema encontra-se em equilíbrio, como mostra a figura.
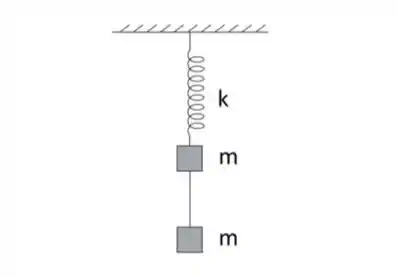
Em um dado instante, corta-se o fio e o sistema formado pela mola e pelo bloco preso em sua extremidade inferior começam a oscilar verticalmente. Supondo desprezíveis todos os atritos e sendo o módulo da aceleração da gravidade, assinale a opção que indica, respectivamente, o período e a amplitude das oscilações harmônicas executadas por esse bloco.
(a) e .
(b) e .
(c) e .
(d) e .
(e) e .
Passo 1
O período depende apenas da massa oscilante, certo? Então:
Sabendo que a amplitude é igual ao deslocamento máximo em relação ao ponto de equilíbrio, ela independe do equilíbrio inicial, ou seja, a massa que foi retirada não é considerada:
Resposta
(a)