A figura mostra um bloco de massa que oscila sobre uma superfície horizontal, sem atrito, sob a ação de uma força elástica produzida por uma mola, da forma:
,
Onde indica a posição horizontal do bloco em um dado sistema de coordenadas, e são constantes e e .
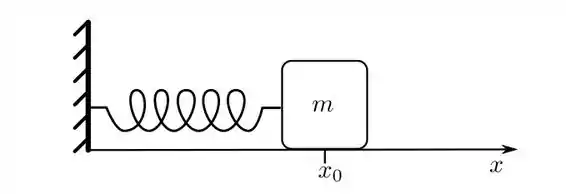
a) Qual a posição de equilíbrio do bloco, , tal que a mola encontra-se relaxada?
b) Encontre a equação diferencial de movimento para a posição do bloco.
c) Encontre a solução geral da equação encontrada no item anterior, sem impor condições iniciais.
d) Encontre a função horária se em o bloco está em e parte do repouso.
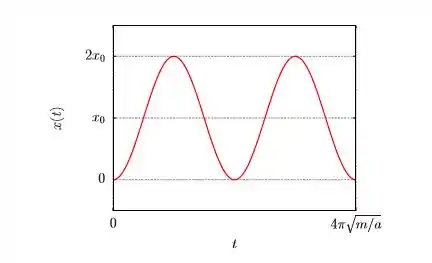
e) Esboce para as primeiras oscilações (decorridos dois períodos) do bloco, respeitando as condições do item . O bloco oscila em torno de que posição?
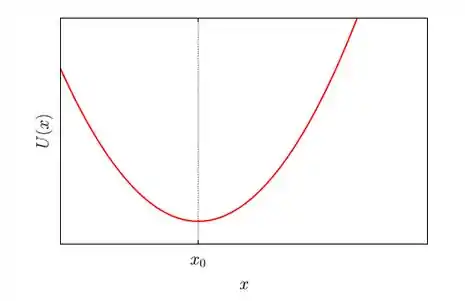
f) Determine a energia potencial elástica para este sistema. Esboce um gráfico para , indicando nele a posição de equilíbrio.
Passo 1
a) Para encontrar a posição em que a mola encontra-se relaxada, aasta achar aquela que a força exercida sobre o bloco é nula:
.
Porque quando a mola tá relaxada não exerce força sobre o objeto, por isso a força é nula.
Logo, .
Passo 2
b) A força resultante no bloco é a força elástica. Então, aplicando a segunda lei de Newton, em que a força resultante é igual a massa vezes aceleração:
Passo 3
c) A solução homogênea da equação anterior satisfaz
,
Cuja solução é da forma:
.
A solução particular pode ser escolhida constante, . Fazendo e substituindo na equação encontramos:
.
A solução geral é, portanto,
.
Passo 4
d) Do enunciado e . Substituindo na solução geral da equação de movimento, com .
,
,
Cuja solução é dada por:
, .
.
Passo 5
e) O bloco oscila em torno de , sua posição de equilíbrio. O gráfico é de duas oscilações completas, começando em seu mínimo, em e e oscilando simetricamente em torno de
Passo 6
f) A energia potencial é dada por
,
,
onde é uma constante arbitrária.
O gráfico é uma parábola com concavidade para cima com seu mínimo em .
Resposta
Ei, a resposta está no passo a passo :)