P2 de Física 2 da USP - 2011

Considere um sistema massa-mola, composto por uma mola de constante e uma massa , sujeito a força de amortecimento proporcional à velocidade dada por . O sistema está no regime crítico de amortecimento.

1. Determine. Em função de e , o valor da constante
2. Sabendo que o sistema parte da posição com velocidade nula, determine a posição do sistema em função do tempo em termos de e
3. Se trocarmos a massa do sistema por qual será o regime de oscilação do sistema? Justifique.
4. Sabendo que a com a nova massa o sistema parte da posição com velocidade nula, determine a posição do sistema em função do tempo em termos de e
5. Se trocarmos agora a massa do sistema por uma massa qual será o novo regime de oscilação do sistema? Justifique.

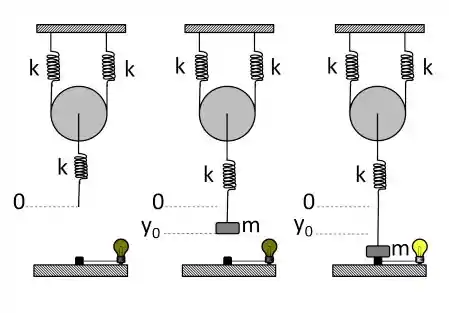
Considere um sistema como o da figura ao lado, composto pro três molas idênticas( com constantes de massas desprezíveis e uma polia, também de massa desprezível. Inicialmente o sistema está em equilíbrio na posição Em um determinado momento, uma massa é conectada a uma das molas, deslocando o sistema do valor Logo desta massa há um dispositivo sensível ao toque que acende uma lâmpada de cada vez que é tocado pela massa. Despreze quaisquer efeitos de atrito no sistema. Supondo que a distância entre a posição de equilíbrio da massa e a superfície do dispositivo sensível ao toque é de e que, para dar início ao movimento, você simplesmente encosta a massa no dispositivo e libera o sistema, calcule:

1. A posição de equilíbrio
2. A equação do movimento resultante da massa
3. A solução da equação do movimento da massa
4. O valor que deve ser escolhido para a massa para que a lâmpada acenda uma vez a cada segundos.
5. O trabalho realizado sobre o sistema em equilíbrio para dar início ao movimento descrito no item .

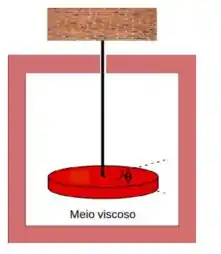
Um pêndulo de torção de massa , imerso em um meio viscoso, oscila em torno do seu ponto de equilíbrio obedecendo a seguinte equação de movimento:

Onde e .

1. Determine a solução da equação do movimento considerando as seguintes restrições e
2. Qual o tempo necessário para que a amplitude caia à metade?

Suponha agora que o pêndulo esteja sob a ação de um torque externo periódico

3. Calcule a amplitude da solução estacionária.
4. Dadas as mesmas condições iniciais do ítem , qual o tempo necessário para que a amplitude da solução transiente seja da amplitude da solução estacionária?