P2 de Física 2 da USP - 2016

Após 6 oscilações, a amplitude de um sistema oscilatório decresce em 10%. Este sistema é formado por uma mola de constante elástica 4500 N/m e um bloco de 90 kg e oscila sobre uma superfície horizontal. O sistema está sujeito à uma força de resistência proporcional à velocidade do bloco. O período de oscilação e a razão entre as energias médias (por ciclo) final e inicial deste sistema, após estas 6 oscilações serão, respectivamente:

1. e
2. e
3. e
4. e
5. e

Um sistema oscilatório tem seu movimento descrito pela seguinte equação:

Onde e B são constantes, são frequências angulares e representa uma fase. Indique qual a afirmativa correta sobre o movimento na condição de ressonância, sabendo que o oscilador está inicialmente em repouso e na posição de equilíbrio:

(a) É uma oscilação sem amortecimento, com no qual a amplitude está crescendo.

(b) É uma oscilação sem amortecimento, com no qual a amplitude está decrescendo.

(c) É uma oscilação com amortecimento forte, com no qual a amplitude está decrescendo.

(d) É uma oscilação com amortecimento, com no qual a amplitude está decrescendo.

(e) É uma oscilação com amortecimento fraco, com no qual a amplitude está decrescendo lentamente.

A figura mostra a posição de um sistema massa-mola sujeito à ação de uma força dissipativa proporcional à velocidade. Sabendo que a massa do bloco é m = 1,0 kg, pode-se afirmar que (dica: considere e lembre-se que e ):

1. A constante de amortecimento é e a frequência natural de oscilação é .
2. A constante de amortecimento é e a frequência natural de oscilação é
3. A constante de amortecimento é e a frequência natural de oscilação é
4. A constante de amortecimento é e a frequência natural de oscilação é
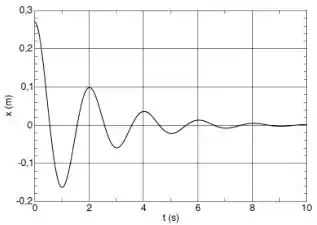
5. A constante de amortecimento é e a frequência natural de oscilação é

Um grupo de estudantes construiu um oscilador utilizando um bloco de massa e uma mola de constante elástica k. Um segundo grupo de estudantes construiu um outro oscilador acoplando um bloco de massa a uma mola idêntica àquela utilizada pelo primeiro grupo de estudantes. Os dois sistemas oscilam em um meio cuja força de resistência é proporcional à velocidade com o mesmo coeficiente de resistência . Cada grupo de estudantes aplicou uma força externa periódica de mesma amplitude aos sistemas. No regime estacionário, os valores máximos das potências médias dissipadas pelos osciladores em cada ciclo de oscilação, são dadas por e . Analisando a curva de ressonância abaixo, pode-se afirmar que:

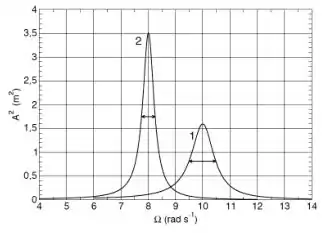
(a) .

(b) .

(c) .

(d) .

(e) .

Um oscilador composto por uma mola de massa desprezível com constante k e por um bloco de massa m, está sujeito à ação de uma força de amortecimento . Considere que o sistema massa-mola se encontra no regime de amortecimento crítico.

a) Determine o coeficiente de resistência viscosa . Forneça a resposta em função de k e m.

(b) Sabendo que as condições iniciais são tais que e , determine a posição do sistema massa-mola em função do tempo. Expresse o resultado em termos de k e m.

(c) Se a massa do bloco dobrar (M = 2m) qual será o regime de oscilação?

(d) Sabendo que as condições iniciais são tais que e , determine a posição do sistema massa-mola em função do tempo. Expresse o resultado em termos de k e m.

Considere um bloco de massa M preso à extremidade de uma mola de constante elástica k e comprimento relaxado e em repouso. A outra extremidade da mola é, então, presa a um dispositivo que oscila com frequência angular e cuja posição é dada por , onde a é uma constante positiva. Suponha que o bloco oscile com a mesma frequência do dispositivo e que o atrito seja desprezível.

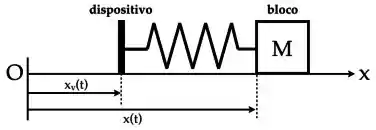
a) Desenhe o diagrama de forças que agem sobre o bloco de massa M e escreva as expressões para os vetores que representam tais forças de forma explícita num sistema de coordenadas apropriado.

(b) Deduza a equação diferencial que descreve o movimento do bloco em termos da variável .

(c) Resolva a equação diferencial encontrando a solução para as condições iniciais do problema.

(d) Qual a frequência do dispositivo para que o sistema entre em ressonância e o que ocorre com a amplitude neste valor de frequência?