P2 de Física 3 - FIS1051 da PUCRIO - 2015.1

Considere o cabo coaxial muito longo da figura ao lado, formado por duas cascas cilíndricas concêntricas com raios internos , e raios externos , , respectivamente. Uma corrente uniforme flui na casca cilíndrica interna com o sentido para fora do plano do papel e uma corrente uniforme com sentido desconhecido flui na casca cilíndrica externa.

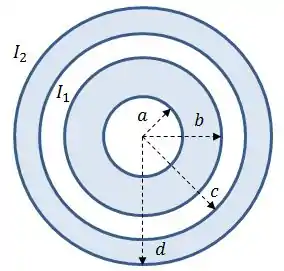
Calcule a intensidade do campo magnético nas regiões:

;

;

;

Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.

Calcule a amplitude do campo magnético em em função da corrente .

No circuito abaixo têm-se:

, , , , , , inicialmente descarregados.

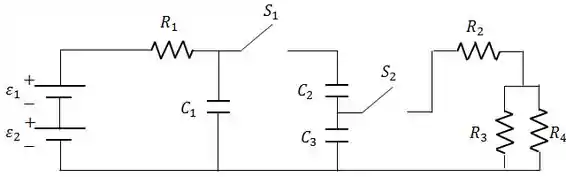
Considere que o circuito tem as seguintes fases sucessivas:

Fase 1: a chave é fechada e permanece aberta durante um tempo muito longo.

Fase 2: a chave é aberta, permanece aberta sendo o meio do capacitor substituído por outro de constante dielétrica duas vezes maior.

Fase 3: a chave permanece aberta e é fechada durante um tempo muito longo.

Determinar:

A carga armazenada em cada capacitor no final da fase 1.

A corrente que passa em em função do tempo durante a fase 1.

A energia fornecida por ambas as baterias durante a fase 1.

A corrente que passa em em função do tempo durante a fase 3.

A energia fornecida por na fase 3.

A potência máxima dissipada em durante a fase 3.

Uma espira com corrente de intensidade tem a forma de dois arcos de circunferência concêntricos unidos por segmentos retilíneos. O arco de menor raio subentende um ângulo , e o raio do outro arco é . Os dois segmentos retilíneos são radiais em relação ao centro C da espira.

Adote o valor .

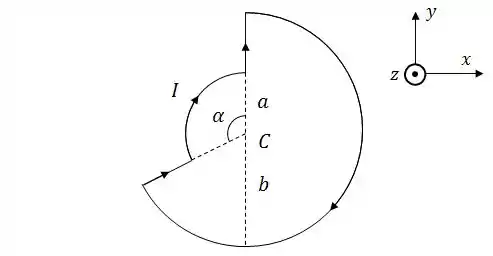
Usando a Lei de Biot-Savart e adotando o sistema de coordenadas da figura, calcule cada uma das contribuições para o vetor campo magnético gerado pela espira em seu centro :

contribuição dos segmentos retilíneos;

contribuição do arco menor;

contribuição do arco maior;

o vetor campo magnético total gerado pela espira em .

Sabendo que um campo magnético externo uniforme e muito intenso, dado por , está presente em toda a região da espira, calcule o vetor torque sobre a espira.

(Nota: use a aproximação ).

Considere agora uma nova situação na qual o campo magnético total em seja dado por , e que uma partícula de carga negativa de módulo passa por com velocidade . Calcule o vetor força magnética sobre a partícula.