Uma espira com corrente de intensidade tem a forma de dois arcos de circunferência concêntricos unidos por segmentos retilíneos. O arco de menor raio subentende um ângulo , e o raio do outro arco é . Os dois segmentos retilíneos são radiais em relação ao centro C da espira.
Adote o valor .
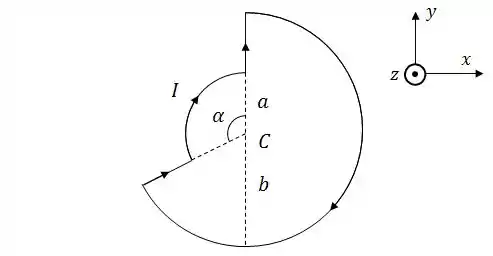
Usando a Lei de Biot-Savart e adotando o sistema de coordenadas da figura, calcule cada uma das contribuições para o vetor campo magnético gerado pela espira em seu centro :
contribuição dos segmentos retilíneos;
contribuição do arco menor;
contribuição do arco maior;
o vetor campo magnético total gerado pela espira em .
Sabendo que um campo magnético externo uniforme e muito intenso, dado por , está presente em toda a região da espira, calcule o vetor torque sobre a espira.
(Nota: use a aproximação ).
Considere agora uma nova situação na qual o campo magnético total em seja dado por , e que uma partícula de carga negativa de módulo passa por com velocidade . Calcule o vetor força magnética sobre a partícula.
Passo 1
contribuição dos segmentos retilíneos;
A Lei de Biot-Savart é dada por:
Onde é um pedaço infinitesimal do segmento cujo vetor aponta sempre na mesma direção e sentido da corrente, e é o vetor unitário que vai do segmento ao ponto onde estamos calculando o campo magnético.
Então vamos começar analisando os vetores e nos segmentos retilíneos:
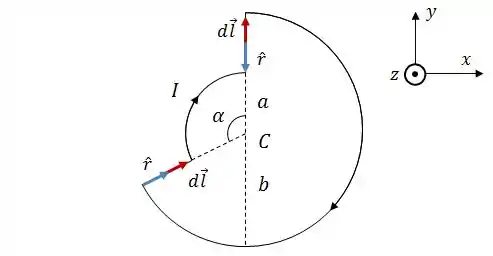
Em ambos os segmentos retilíneos, os vetores e são colineares... isso significa que:
Assim, a contribuição dos segmentos retilíneos será:
Passo 2
contribuição do arco menor;
Novamente, vamos começar analisando os vetores e no arco menor:
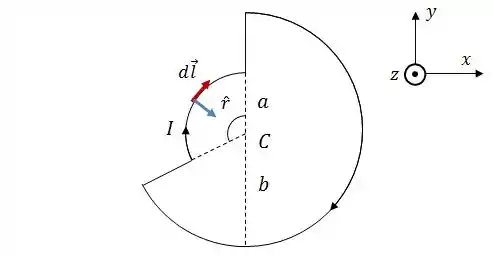
Nesse caso, como é sempre tangente ao arco e aponta para o centro do arco, os dois serão sempre perpendiculares, para qualquer ponto. Logo, através da regra da mão direita:
Aplicando isso à Lei de Biot-Savart onde e são constantes, teremos:
Onde será igual ao comprimento do arco:
Substituindo os valores de , e , teremos:
Passo 3
contribuição do arco maior;
Novamente, vamos começar analisando os vetores e no arco maior:
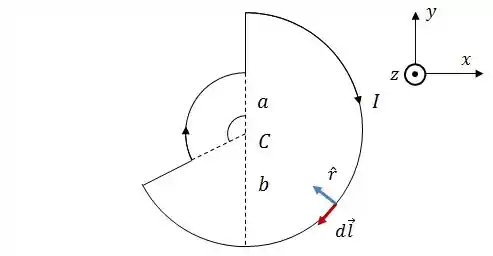
Nesse caso, como é sempre tangente ao arco e aponta para o centro do arco, os dois serão sempre perpendiculares, para qualquer ponto. Logo, através da regra da mão direita:
Aplicando isso à Lei de Biot-Savart onde e são constantes, teremos:
Onde será igual ao comprimento do arco, que será o produto do raio do arco maior com o ângulo de abertura do arco maior:
Substituindo os valores de , e , teremos:
Passo 4
o vetor campo magnético total gerado pela espira em .
O campo magnético total no ponto será a soma dos campos magnéticos gerados pelos segmentos retilíneos e os arcos, logo:
Passo 5
Sabendo que um campo magnético externo uniforme e muito intenso, dado por , está presente em toda a região da espira, calcule o vetor torque sobre a espira.
O torque magnético sobre a espira é dada por:
Onde é o vetor campo magnético, dado por:
Onde é o vetor cujo módulo é a área da espira e a direção e sentido são determinados através da regra da mão direita, de acordo com o sentido da corrente:
Substituindo os valores de e , e adotanto (de acordo com o enunciado), teremos:
Assim, o momento magnético será dado por:
Finalmente, o torque magnético será dado por:
Passo 6
Considere agora uma nova situação na qual o campo magnético total em seja dado por , e que uma partícula de carga negativa de módulo passa por com velocidade . Calcule o vetor força magnética sobre a partícula.
A força magnética sobre uma partícula carregada é dada por:
Substituindo os valores:
Resposta