No circuito abaixo têm-se:
, , , , , , inicialmente descarregados.
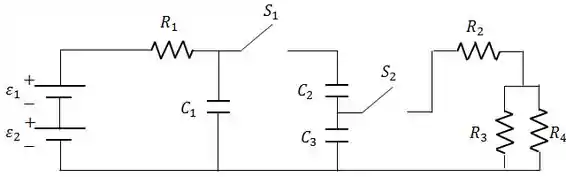
Considere que o circuito tem as seguintes fases sucessivas:
Fase 1: a chave é fechada e permanece aberta durante um tempo muito longo.
Fase 2: a chave é aberta, permanece aberta sendo o meio do capacitor substituído por outro de constante dielétrica duas vezes maior.
Fase 3: a chave permanece aberta e é fechada durante um tempo muito longo.
Determinar:
A carga armazenada em cada capacitor no final da fase 1.
A corrente que passa em em função do tempo durante a fase 1.
A energia fornecida por ambas as baterias durante a fase 1.
A corrente que passa em em função do tempo durante a fase 3.
A energia fornecida por na fase 3.
A potência máxima dissipada em durante a fase 3.
Passo 1
A carga armazenada em cada capacitor no final da fase 1.
Com a chave fechada e a chave aberta, o circuito é, basicamente, este:
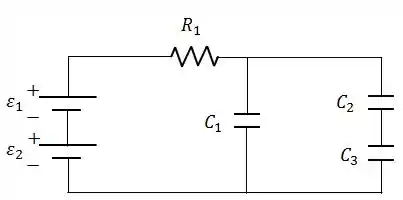
Quando o problema diz que essa situação permanece assim por um longo tempo, ele quer dizer que no final da fase 1 os capacitores estarão carregados.
Quando os capacitores ficarem completamente carregados, a corrente no circuito será nula, isso significa que não teremos diferença de potencial devido o resistor . Além disso, os dois ramos de capacitores (um com e o outro om e ) terão a mesma diferença de potencial, já que estão em paralelo.
Capacitor :
Capacitor e :
O primeiro passo aqui é começar calculando a capacitância equivalente entre esses caras. Como eles estão em série, a capacitância equivalente será:
Logo:
Como e estão em série:
Passo 2
A corrente que passa em em função do tempo durante a fase 1.
Quando o problema fala “durante a fase”, ele está se referindo ao processo de carregamento dos capacitores.
Durante o carregamento, a corrente no circuito será:
Então, o que temos que fazer aqui é calcular a capacitância equivalente do circuito.
Na letra , nós calculamos a capacitância equivalente referente aos capacitores em série e . Logo, como e estão em paralelo, a capacitância equivalente será dada por:
Portanto, a corrente que passa por será:
Passo 3
A energia fornecida por ambas as baterias durante a fase 1.
A potência fornecida por ambas as baterias é dada por:
Por definição, potência e energia estão relacionados por:
Logo:
Finalmente:
Passo 4
A corrente que passa em em função do tempo durante a fase 3.
Antes de irmos direto para a fase 3, vamos dar uma olhada no que aconteceu na fase 2.
Na fase 2, nós mudamos o capacitor por outro de constante dielétrica duas vezes maior, logo:
Lembrando que o capacitor continua carregado, conforme o final da fase 1.
Agora, na fase 3, quando mantemos a chave aberta e fechamos a chave , o capacitor vai entrar em processo de descarga, e o circuito será, basicamente este:
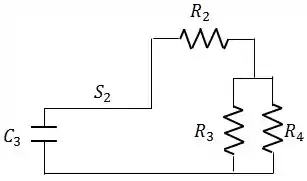
A corrente durante o descarregamento do capacitor será:
Beleza. A única coisa que não temos daqui é a resistência equivalente. Pra calculá-la, vamos começar pelos resistores e , que estão em paralelo.
Assim, a resistência equivalente será:
Assim, a corrente que passa pelo resistor 2 será:
O sinal negativo apenas denota o sentido em que a corrente está se deslocando. Assim, o módulo da corrente que passa por será:
Passo 5
A energia fornecida por na fase 3.
Aqui, a energia fornecida por será toda a energia armazenada no capacitor no início da fase 3, logo:
Passo 6
A potência máxima dissipada em durante a fase 3.
A potência dissipada em um resistor é dada por:
Como queremos calcular a potência máxima dissipada em :
Resposta