Considere o cabo coaxial muito longo da figura ao lado, formado por duas cascas cilíndricas concêntricas com raios internos , e raios externos , , respectivamente. Uma corrente uniforme flui na casca cilíndrica interna com o sentido para fora do plano do papel e uma corrente uniforme com sentido desconhecido flui na casca cilíndrica externa.
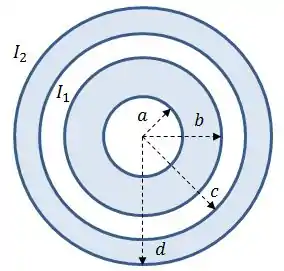
Calcule a intensidade do campo magnético nas regiões:
;
;
;
Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.
Calcule a amplitude do campo magnético em em função da corrente .
Passo 1
;
Esse é um problema clássico de Lei de Ampère, dada por:
Podemos dar uma simplificada na expressão acima:
Onde a integral será igual ao comprimento da nossa amperiana que, nesse caso, será uma circunferência de raio :
Assim, para cada caso, o nosso único trabalho é calcular a corrente englobada pela amperiana.
A amperiana de raio não engloba nenhuma corrente, logo:
Passo 2
;
A amperiana com esse raio engloba apenas parte da primeira casca cilíndrica.
Como a corrente é uniformemente distribuída pela sessão transversal da casca cilíndrica, podemos determinar com uma regra de 3:
Substituindo na expressão do campo magnético, teremos:
Passo 3
;
A amperiana com esse raio engloba toda a primeira casca cilíndrica, logo:
Logo:
Passo 4
Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.
Vamos usar a Lei de Ampère para calcular o campo elétrico a uma distância do centro.
Novamente, o campo magnético terá essa cara:
Esse campo magnético deve ser igual ao campo dado pelo enunciado, logo:
Simplificando:
Agora, o nosso trabalho é calcular a corrente englobada pela amperiana de raio .
Passo 5
A amperiana vai englobar toda a casca cilíndrica de corrente e parte da casca cilíndrica externa.
Logo:
Pra determinar , vamos fazer o mesmo que fizemos anteriormente, calculando através de uma regra de 3:
Portanto:
Voltando ao problema:
Finalmente:
Passo 6
Calcule a amplitude do campo magnético em em função da corrente .
Esse raio engloba as duas cascas cilíndricas, logo:
Assim, o campo magnético será dado por:
Resposta