P4 de Física 3 - FIS1051 da PUCRIO - 2013.1

O valor do módulo do campo elétrico presente na superfície de uma esfera condutora de raio , mostrada na figura abaixo, é igual a . O campo elétrico aponta para o interior da esfera.

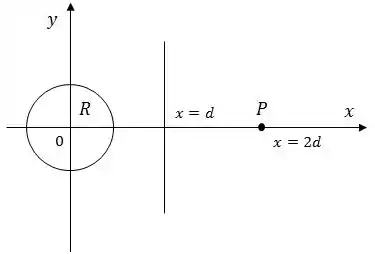
Calcule a carga resultante na superfície da esfera (deixe o resultado em função de e ).

Considere agora que um anel isolante uniformemente carregado com carga total igual a é colocado numa distância do centro da esfera como indicado na figura acima (o anel é visto de perfil).

Sabendo que o raio do anel é , calcule o vetor campo elétrico resultante no ponto de coordenada (deixe o resultado em função de ).

Um fio extremamente longo é dobrado na forma mostrada na figura, de forma a evitar o contato no ponto de cruzamento . O raio da parte circular é e a corrente tem o sentido indicado.

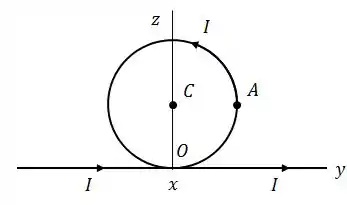
Determine a contribuição da parte linear do fio para o vetor campo magnético no centro e no ponto do círculo.

Determine a contribuição da parte circular do fio para o vetor campo magnético no centro do círculo e o vetor campo magnético total no mesmo ponto.

Em seguida, a parte circular do fio é girada de , sem distorção, em torno do eixo , tornando-se perpendicular à parte linear, de tal forma que a nova posição do ponto tem coordenada positiva.

Determine uma expressão para o vetor campo magnético total no centro do círculo.

A figura ao lado mostra uma barra de comprimento que se move com velocidade constante ao longo de trilhos paralelos ao eixo , conectados por um segmento contido no eixo . Os trilhos e o segmento são condutores, fixos e indeformáveis e o plano é horizontal. No eixo existe um fio muito comprido percorrido por uma corrente que cria um campo magnético não uniforme dado pela Lei de Ampère.

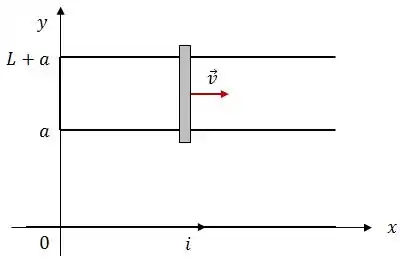
Encontre a força eletromotriz induzida na barra.

Supondo que a resistência da barra vale e as dos trilhos e do segmento são desprezíveis, calcule a corrente induzida e indique o seu sentido.

Calcule a força realizada por um agente externo para manter a barra se deslocando com velocidade constante. Indique o sentido da força externa.

Considere o circuito ao lado com , , , e . O capacitor está inicialmente descarregado.

A chave é fechada para , produzindo uma corrente que passa através do ramo do indutor e uma corrente que passa através do ramo do capacitor.

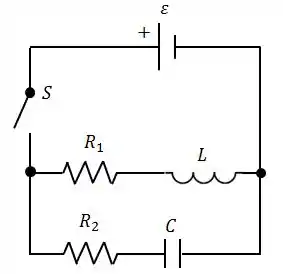
Calcule o valor de e no instante e o valor de e após um tempo muito grande após o fechamento da chave .

Escreva (indicando os valores) o comportamento das correntes e em função do tempo (a partir de ), levando em conta as diferentes constantes de tempo de cada ramo. Faça um gráfico destas correntes.

Após um tempo muito longo, a chave é aberta de novo. Desenhe o gráfico do comportamento de em função do tempo a partir da abertura de .

Qual é o valor da energia total dissipada nos dois resistores e ?