Considere o circuito ao lado com , , , e . O capacitor está inicialmente descarregado.
A chave é fechada para , produzindo uma corrente que passa através do ramo do indutor e uma corrente que passa através do ramo do capacitor.
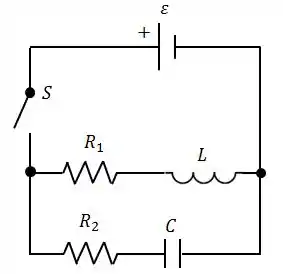
Calcule o valor de e no instante e o valor de e após um tempo muito grande após o fechamento da chave .
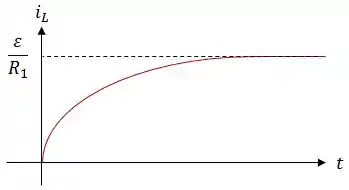
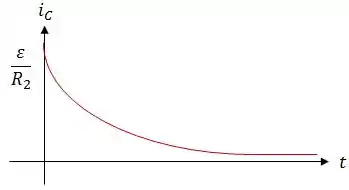
Escreva (indicando os valores) o comportamento das correntes e em função do tempo (a partir de ), levando em conta as diferentes constantes de tempo de cada ramo. Faça um gráfico destas correntes.
Após um tempo muito longo, a chave é aberta de novo. Desenhe o gráfico do comportamento de em função do tempo a partir da abertura de .
Qual é o valor da energia total dissipada nos dois resistores e ?
Passo 1
Calcule o valor de e no instante e o valor de e após um tempo muito grande após o fechamento da chave .
- :
- :
- :
- :
No instante inicial, o indutor funciona como se o circuito aberto e o capacitor funciona como curto circuito, logo:
Após um intervalo de tempo muito grande, os dois têm comportamentos opostos. O indutor funciona como curto circuito, e o capacitor funciona como circuito aberto.
Passo 2
Escreva (indicando os valores) o comportamento das correntes e em função do tempo (a partir de ), levando em conta as diferentes constantes de tempo de cada ramo. Faça um gráfico destas correntes.
A malha com os elementos , e é um circuito . Nele, a corrente no indutor varia de acordo com a equação:
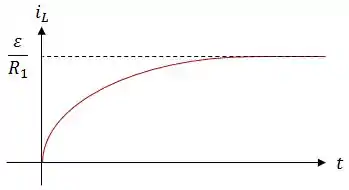
E a malha com os elementos , e é um circuito onde a carga do capacitor, durante o seu carregamento, obedece a seguinte equação:
Assim, a corrente através do capacitor será dada por:
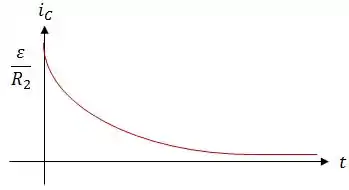
Passo 3
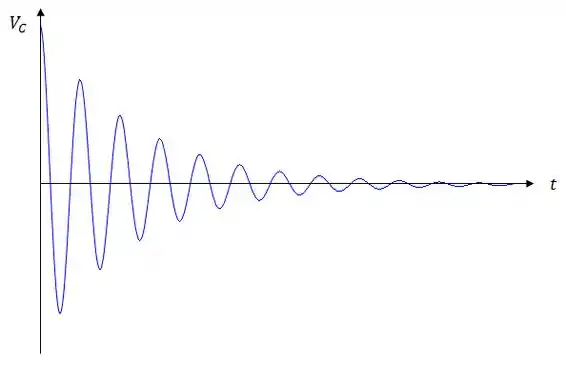
Após um tempo muito longo, a chave é aberta de novo. Desenhe o gráfico do comportamento de em função do tempo a partir da abertura de .
Após um tempo muito longo, o capacitor estará completamente carregado e, quando a chave for aberta, os elementos , , , e formarão um circuito .
De acordo com a lei das malhas, teríamos:
Onde .
Essa função lembra bastante a equação para um oscilador amortecido, que você já deve ter visto em algum momento da sua vida.
Pois bem, aqui, a função terá a mesma cara. E como:
A tensão no capacitor será uma função oscilatória amortecida. Resumidamente, ela vai ter essa cara:
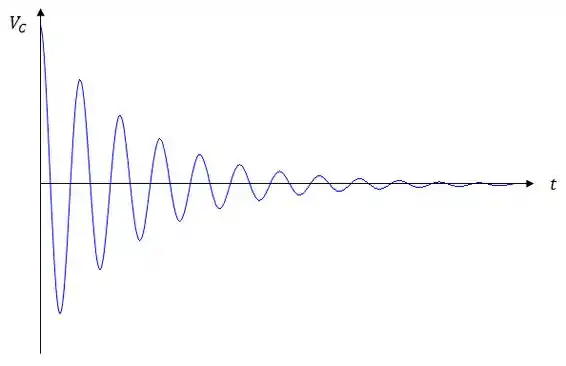
Obs.: Como o capacitor está carregado quando a chave é aberta, a tensão no capacitor em é máxima.
Passo 4
Qual é o valor da energia total dissipada nos dois resistores e ?
Nesse circuito, apenas e dissipam a energia do sistema. Assim, a energia total dissipada pelos resistores deve ser igual à energia armazenada no indutor e no capacitor.
Logo:
Onde a corrente máxima no indutor será .
Sabendo que , , e e substituindo os valores, teremos:
Resposta
Resposta
Ei, a resposta está no passo a passo :)