Densidade de Carga, Campos Elétricos e Corpos Carregados, Lei de Gauss
O valor do módulo do campo elétrico presente na superfície de uma esfera condutora de raio , mostrada na figura abaixo, é igual a . O campo elétrico aponta para o interior da esfera.
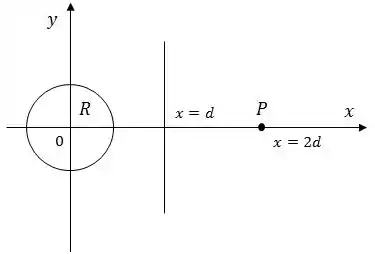
Calcule a carga resultante na superfície da esfera (deixe o resultado em função de e ).
Considere agora que um anel isolante uniformemente carregado com carga total igual a é colocado numa distância do centro da esfera como indicado na figura acima (o anel é visto de perfil).
Sabendo que o raio do anel é , calcule o vetor campo elétrico resultante no ponto de coordenada (deixe o resultado em função de ).
Passo 1
Calcule a carga resultante na superfície da esfera (deixe o resultado em função de e ).
O problema nos deu o raio da esfera e o campo elétrico na sua superfície, então, pra descobrirmos o valor da carga, basta usar a lei de Gauss, dada por:
Devido à simetria do problema, a nossa gaussiana será uma esfera de raio , que engloba toda a esfera.
Obs.: Como o campo elétrico aponta para dentro da esfera, isso significa que a carga é negativa, logo:
Onde:
Finalmente:
Passo 2
Sabendo que o raio do anel é , calcule o vetor campo elétrico resultante no ponto de coordenada (deixe o resultado em função de ).
O campo elétrico resultante no ponto será a soma vetorial dos campos da esfera e do anel.
Então vamos calcular cada um separadamente:
- :
- :
O campo elétrico gerado pela esfera no ponto é determinado pela lei de Gauss, onde a gaussiana, nesse caso, será uma esfera de raio , que é a distância entre o centro da esfera e o ponto , logo:
Como o campo elétrico te direção radial, no ponto , o vetor campo elétrico gerado pela esfera será:
Onde , logo:
Passo 3
Para calcular o campo elétrico gerado pelo anel, vamos começar escrevendo a expressão do campo elétrico gerado por um pedaço infinitesimal do anel, de carga :
Vamos pegar dois pontos simétricos do anel, ambos de carga , e ver o campo elétrico resultante no ponto .
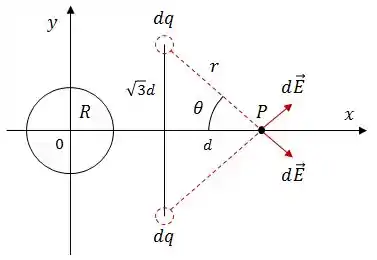
Consegue ver que as componentes perpendiculares a vão se anular e as componentes paralelas a vão se somar?
Isso vai acontecer para cada par de pontos simétricos, logo, o resultado disso é que o campo elétrico gerado pelo anel terá apenas componente na direção do eixo , isso significa que não precisamos nos preocupar com as outras direções.
Além disso, da imagem acima, podemos tirar que:
Logo:
Agora basta integrar esse cara em relação a , onde :
A densidade linear de carga é dada por:
Logo:
Onde , logo:
Passo 3
Finalmente, o campo elétrico resultante no ponto será:
Resposta