A figura ao lado mostra uma barra de comprimento que se move com velocidade constante ao longo de trilhos paralelos ao eixo , conectados por um segmento contido no eixo . Os trilhos e o segmento são condutores, fixos e indeformáveis e o plano é horizontal. No eixo existe um fio muito comprido percorrido por uma corrente que cria um campo magnético não uniforme dado pela Lei de Ampère.
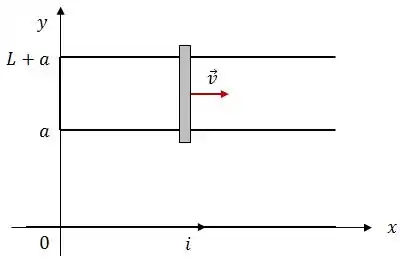
Encontre a força eletromotriz induzida na barra.
Supondo que a resistência da barra vale e as dos trilhos e do segmento são desprezíveis, calcule a corrente induzida e indique o seu sentido.
Calcule a força realizada por um agente externo para manter a barra se deslocando com velocidade constante. Indique o sentido da força externa.
Passo 1
Encontre a força eletromotriz induzida na barra.
Vamos ter que passar por algumas etapas antes de encontrar a induzida... vamos nessa.
A induzida é determinada pela lei de Faraday, dada por:
Beleza, então vamos precisar calcular o fluxo magnético, que é dado por:
Pra isso vamos precisar calcular o campo magnético gerado pelo fio, que é dado através da lei de Ampère:
Acabou, esse são, basicamente, os três passos que vamos ter que seguir para calcular a induzida na barra, ok?
Passo 2
Vamos começar calculando o campo magnético gerado pelo fio para (que é onde está a espira).
A amperiana aqui será uma circunferência de raio que engloba o fio de corrente , logo:
De acordo com a regra da mão direita, o campo magnético, na região da espira, estará saindo do plano da página:
Passo 3
O fluxo magnético é dado por:
O elemento de área será:
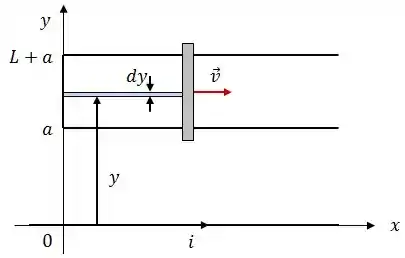
Logo:
Passo 4
Finalmente, a induzida será:
Substituindo a expressão de que acabamos de calcular, teremos:
Onde , logo:
Passo 5
Supondo que a resistência da barra vale e as dos trilhos e do segmento são desprezíveis, calcule a corrente induzida e indique o seu sentido.
A corrente induzida será dada por:
Logo:
O sentido da corrente é determinado pela lei de Lenz, que diz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela diz é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
O fluxo magnético é dada por:
A derivada temporal do fluxo magnético será:
Sendo assim, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Como o campo magnético externo está no sentido do vetor , o campo magnético induzido estará no sentido oposto, ou seja, no sentido do vetor , entrando no plano da página.
De acordo com a regra da mão direita, para que o campo magnético induzido esteja entrando no plano da página, a corrente induzida deve estar no sentido horário.
Passo 6
Calcule a força realizada por um agente externo para manter a barra se deslocando com velocidade constante. Indique o sentido da força externa.
A força externa deve ter o mesmo módulo e direção da força magnética gerada sobre a barra , porém, as duas devem ter sentidos opostos.
A força magnética sobre a barra será dada por:
Onde deve ter a mesma direção e sentido da corrente na barra (que está no sentido horário):
Substituindo esses caras na expressão de , teremos:
Conforme dissemos anteriormente:
Resposta
A corrente induzida estará no sentido horário.