P4 de Física 3 - FIS1051 da PUCRIO - 2020.2

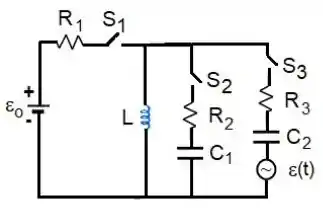
Muito tempo após o fechamento da chave , ela é aberta e, simultaneamente, apenas a chave é fechada, dando início à FASE 2 (a chave continua aberta). Observou-se que a corrente no circuito relevante varia em função do tempo (medido em segundos a partir do início da FASE 2) de acordo com a expressão , sendo e , tendo sentido consistente com o determinado no item (a). Observe que resulta da derivada em relação ao tempo da expressão para a carga no capacitor C1: . Com base nestas informações:

c) Determine os valores de e .

d) Determine o valor do módulo das cargas iniciais no capacitor , indicando se a carga positiva está na sua placa superior ou inferior.

Duas esferas condutoras sólidas em equilíbrio eletrostático, de raios respectivos e , estão carregadas com cargas e respectivamente. Estas esferas estão colocadas a uma grande distância uma da outra de modo que o efeito da carga de uma esfera não interfere com a carga da outra.

d) Calcule o potencial eletrostático de cada esfera, assim como o campo elétrico na superfície de cada uma.

Conectando as duas esferas por um fio condutor perfeito muito fino atingimos um novo equilíbrio eletrostático.

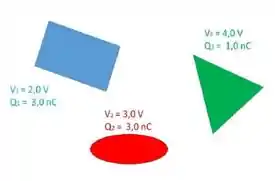
e) Nesta nova situação, calcule as cargas de cada esfera.

Três objetos sólidos condutores perfeitos 1, 2 e 3, como visto na figura, tem potenciais , e cargas líquidas . Os sólidos estão em equilíbrio eletrostático e não se tocam.

f) Calcule a energia eletrostática total do sistema formado pelos condutores 1, 2 e 3.

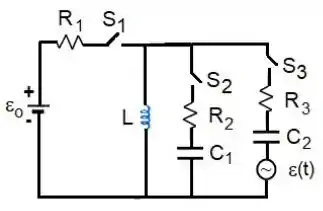
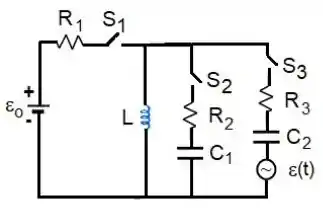
No circuito da Figura, os elementos conhecidos têm os seguintes valores: , , , e . Inicialmente, todas as chaves estão abertas, o capacitor tem uma carga desconhecida, o capacitor está descarregado e não existe corrente no indutor . Na FASE 1, apenas a chave é fechada. Imediatamente após o fechamento desta chave, mede-se a corrente A no circuito relevante, sendo o tempo expresso em segundos. Com base nestas informações:

a) Determine os valores de e , indicando o sentido da corrente no circuito (horário ou anti-horário) muito tempo após o fechamento da chave .

b) Calcule a energia armazenada no indutor L muito tempo após o fechamento da chave .

Três cascas esféricas concêntricas, de raios e respectivamente, são feitas de um material condutor perfeito de espessura desprezível. Em cada casca esférica está colocada a mesma quantidade de carga elétrica líquida igual a Q. As cascas esféricas estão em equilíbrio eletrostático. Não considere nenhuma outra carga na vizinhança das cascas esféricas ao responder às questões abaixo. Considere o centro do sistema de coordenadas coincidindo com o centro das cascas esféricas.

1. Faça um desenho do sistema incluindo as cascas esféricas e os eixos de coordenadas.
2. Calcule o vetor campo elétrico ao longo do eixo para as situações:

• ;
• ;
• ;

Muito tempo após o fechamento da chave , ela é aberta e, simultaneamente, apenas a chave é fechada, dando início à FASE 3 (a chave continua aberta). Nos itens seguintes, suponha que .

e) Desenhe o diagrama fasorial correspondente ao circuito relevante em escala, apresentando os valores dos fasores . Indique se o circuito é indutivo, capacitivo ou ressonante. Justifique sua resposta. Calcule o ângulo de fase entre e

C A ao circuito e a potência média dissipada em .

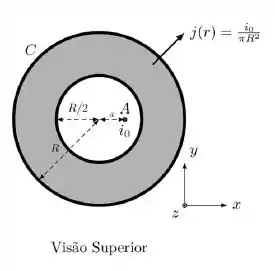
Um fio A de comprimento muito grande é percorrido por uma corrente no sentido positivo do eixo-z, como mostra a figura. Esse fio está envolto por uma casca cilíndrica , também de comprimento, de raio interno e raio externo . A corrente que percorre a casca cilíndrica não é homogênea, obedecendo a uma densidade de corrente ,onde é a distância com relação ao centro do cilindro.

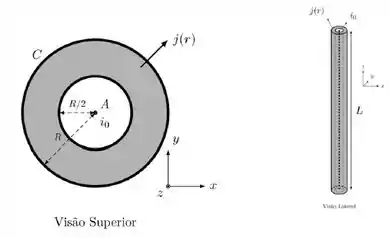
a) Considere que a densidade de corrente do fio é onde é desconhecido.

Encontre o valor de j0 para que o campo magnético possua um valor constante na região interior da casca cilíndrica e encontre a magnitude desse campo (não se esqueça de considerar também a influência do campo do fio no interior). Encontre também qual a direção da corrente (z positivo ou z negativo).

b) Considere que a densidade de corrente é no eixo-z positivo (diferente do item (a). Se aplicamos na região do espaço um campo magnético constante na direção positiva do eixo x, calcule o vetor força magnética resultante na casca cilíndrica C devido ao campo magnético aplicado. Sugestão: considere que a casca é na realidade composta por diversos fios finos de corrente infinitesimal .

c) Considere que a densidade de corrente é agora constante e que o fio A foi deslocado de a com relação ao centro, como mostra a nova figura. Encontre a força magnética que o a casca C realiza no fio A. Justifique sua resposta com cálculos.