Um fio A de comprimento muito grande é percorrido por uma corrente no sentido positivo do eixo-z, como mostra a figura. Esse fio está envolto por uma casca cilíndrica , também de comprimento, de raio interno e raio externo . A corrente que percorre a casca cilíndrica não é homogênea, obedecendo a uma densidade de corrente ,onde é a distância com relação ao centro do cilindro.
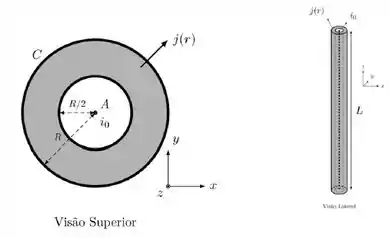
a) Considere que a densidade de corrente do fio é onde é desconhecido.
Encontre o valor de j0 para que o campo magnético possua um valor constante na região interior da casca cilíndrica e encontre a magnitude desse campo (não se esqueça de considerar também a influência do campo do fio no interior). Encontre também qual a direção da corrente (z positivo ou z negativo).
b) Considere que a densidade de corrente é no eixo-z positivo (diferente do item (a). Se aplicamos na região do espaço um campo magnético constante na direção positiva do eixo x, calcule o vetor força magnética resultante na casca cilíndrica C devido ao campo magnético aplicado. Sugestão: considere que a casca é na realidade composta por diversos fios finos de corrente infinitesimal .
c) Considere que a densidade de corrente é agora constante e que o fio A foi deslocado de a com relação ao centro, como mostra a nova figura. Encontre a força magnética que o a casca C realiza no fio A. Justifique sua resposta com cálculos.
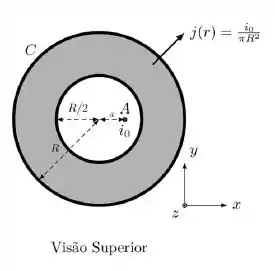
Passo 1
Fala galera, tudo bem? Vou ajudar você aqui!
Letra (a):
Vou começar calculando o campo com a lei de Ampére:
E a corrente envolvida é calculada separadamente:
Daí o campo é:
Beleza?
O campo total é:
O primeiro e o terceiro termos devem se anular, então:
E daí temos :
E podemos calcular :
A direção é .
Passo 2
Letra (b):
A força que um pedacinho de fio faz é:
Como e são constantes, a força sobre um condutor vai ser:
Passo 3
Agora vou calcular a corrente total . Usando a densidade de corrente dada, temos:
Daí a força é:
Tranqüilo até aqui?
Vamos para o último item?
Passo 4
Letra (c):
Usando a lei de Ampére dentro da casca:
Mas , então:
E a força:
Beleza?
Espero ter te ajduado!